Sorry, about the slightly messy notation, but I'm still trying to figure out how to use this thing.
Ok, I assume the thing that's making it tricky for you is the rather nastly looking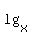 
. When I first saw this problem I thought eugh! What on earth am I going to do with that. I then remembered somebody's (probably not) famous theorem.
Logs of different bases differ by a multiplicitive constant!
Let me demonstrate this with an example, say we wanted to solve 
. I'm sure you could tell me straight away that the answer is 
. But let's try and work out the answer another way. Lets take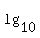 
of both sides of the equation.
Applying one of the many "laws of logs"
And finally dividing
So, we've solved for 
in two different ways, and thus we have worked out that
Now if you can do the same thing and turn the nasty 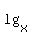into a much nicer 
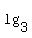you should be able to do the problem.
There is another possibly tricky bit, but see how you get on. please write back if you didn't follow that, or you get stuck further on.
Hope that helps
Kev
(