SOLUTION: Prove that cos^2 theta / (cot^2 theta - cos^2 theta) = 3

Algebra ->  Trigonometry-basics -> SOLUTION: Prove that cos^2 theta / (cot^2 theta - cos^2 theta) = 3      Log On


   

Question 239784: Prove that
cos^2 theta / (cot^2 theta - cos^2 theta) = 3
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Before we start a few of notes:
  • Algebra.com's formula software for some reason does not "do" theta. So I will be using just "t" instead of theta.
  • Algebra.com's formula software does not handle powers of functions well. You may see some multiplication symbols, "*", between the function and the arguments. These multiplication symbols are not correct and should not be there.
  • There are two kinds of equations in Trig.:
    • Identities which are equations which are true for all possible angles. These are the equations you "prove".
    • Conditional equations which are true for only some angles. These equations you solve to find the angles which make the equation true.
    The equation you have in this problem is a conditional equation not an identity. So we will not prove it. We will solve it.

Whether you are proving an identity or trying to solve a conditional equation, if the path is not clear to you it is often a good idea to change other Trig functions into sin's and cos's. This is where we will start. Since cot(t) = cos(t)/sin(t)
cos%5E2%28t%29%2F+%28cot%5E2%28t%29+-+cos%5E2%28t%29%29+=+3
becomes, after replacing 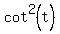cot%5E2%28t%29:
cos%5E2+%28t%29%2F+%28%28cos%5E2+%28t%29%2Fsin%5E2%28t%29%29+-+cos%5E2+%28t%29%29+=+3
Since every term in both the numerator and denominator of the fraction has cos%5E2%28t%29 in it, the fraction will simplify greatly if we multiply the numerator and denominator by its reciprocal:

All the cos%5E2%28t%29's cancel leaving:
1%2F%281%2Fsin%5E2%28t%29+-+1%29+=+3
Now we can further simplify the left side by multiplying the numerator and denominator by 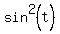sin%5E2%28t%29:
%281%2F%281%2Fsin%5E2%28t%29%29+-+1%29%28sin%5E2%28t%29%2Fsin%5E2%28t%29%29+=+3
which gives us:
sin%5E2%28t%29%2F%281-sin%5E2%28t%29%29+=+3
The denominator should look familiar. It is cos%5E2%28t%29:
sin%5E2%28t%29%2Fcos%5E2%28t%29+=+3
The left side is 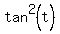tan%5E2%28t%29:
tan%5E2%28t%29+=+3
We now have the equation in a form we can solve. (Up to this point, all we've been doing is "playing around" with the equation, using Algebra and Trig. properties/identities, until we find an equation we can solve.)

If tan%5E2%28t%29+=+3 then
tan%28t%29+=+sqrt%283%29 or tan%28t%29+=+-sqrt%283%29
If you know your special angle values well you will recognize that the reference angle is 60 degrees or pi%2F3 radians. Since theta is normally used for angles measured in degrees, we will use 60 degrees. So the solution is:
t+=+60+%2B+180n or t+=+-60+%2B+180n
Notes about the solution:
  • The "+ 180n"
    • Trig functions are periodic and so when finding angles, there will be an infinite number of solutions. And our solution should reflect all the angles which fit. The "+ 180n" is used as a way to specify this infinite set of angles.
    • The "n" can be any integer.
    • The "180" is used because the period of the tan function is 180 degrees. (For sin, cos, sec and csc we would use 360.)
  • The "60". Any angle with a tan of sqrt%283%29 could be used. 60 is the most "obvious".
  • The "-60". Any angle with a tan of -sqrt%283%29 could be used. -60, 120 or 300 are probably the most "obvious".