Question 239120: Find the LCM
z^3+4z^2+4z, z^2-4z
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Whether you are working with just plain numbers or with expressions, you find LCM's the same way: You factor the numbers or expressions and use those factors to find the LCM.
So we start by factoring and you always start factoring with the Greatest Common Factor (GCF). The GCF of 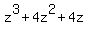 is z so we can factor it into: is z so we can factor it into:

Then the second factor fits the perfect square trinomial pattern,  , where the "a" is "z" and the "b" is "2". So it will factor into , where the "a" is "z" and the "b" is "2". So it will factor into  : :

Now we'll factor 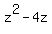 . (Was this supposed to be . (Was this supposed to be 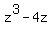 ? If so, the problem is a bit more interesting. Just in case, I'll solve using this, too, at the end.) Again we start with the GCF (which is z again): ? If so, the problem is a bit more interesting. Just in case, I'll solve using this, too, at the end.) Again we start with the GCF (which is z again):

And this is all the factoring we can do.
So we have

and

To find the LCM you find the product of every different factor. In the case of any common factors, use the higher exponent on those factors. Between these two factored expressions, we have 3 different factors: z, z+2 and z-4. z is a factor common to both. In both factored expressions, the exponent on z is 1 so the "higher" exponent is 1. So the LCM is

If your answer is supposed to be simplified, you'll need to multiply this out.
In case the second expression was supposed to be 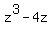 , then it factors this way: , then it factors this way:

The second factor is a difference of squares so it factors:

So the LCM between

and

would be
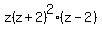
(Note how, with the z+2 factor, we used the higher exponent in the LCM).
|
|
|