Question 238720: What is the largest possible product of a set of positive integers whose sum is 20?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I'm assuming the problem is about 2 positive integers and that you are not looking for a solution that uses Calculus. If I am wrong about either assumption then stop reading and be more specific when you repost your question.
When you do word problems, it is often to your advantage to use as few variables as possible. So if we say
Let x = one of the positive integers
we could use an entirely separate variable for the other positive integer. Or we could take advantage of the fact that the two integers add up to 20 and say
then (20-x) = the other integer
(If if is not clear to you why (20-x) works, Just add x and (20-x) and see what you get.) Using the x and (20-x), the product becomes:
x(20-x)
If we multiply this out we get:
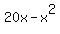
or
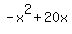
So the question is now, what is the largest value this can be? If we call this y then
and we have the equation of a parabola. Because of the negative coefficient in front of  this parabola opens downward. If you can picture such a parabola, you will realize that the highest point (which would be the highest product since that is what y represents) would be the vertex of this parabola. So if we can find the vertex we can find the value for x that makes the product the largest it can possibly be.
The vertex of a parabola can be found in different ways. One way is to use the fact that for the general parabola,  , the vertex will be where x = -b/2a. For our equation, , b = 10 and a = (-1) so the vertex will be when x = -(20)/(2(-1)) = 10. And this makes the other positive integer, 20-x, also 10.
P.S. Another way to find the vertex is to transform the equation into the form:
In a parabola in this form, the vertex is (h, k). To transform , we start by factoring out -1:
Next we complete the square in the parentheses. Since half of 20 is 10 and 10 squared is 100, we want the expression in the parentheses to be 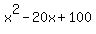 . In order to add the 100 inside the parentheses on the right side, we need to realize that, because of the -1 outside the parentheses, that we are actually adding -100 to the right side when we put a 100 inside the parentheses. And if we add -100 to the right side, we need to add -100 to the left side, too. This gives us:
By completing the square we can now rewrite the expression in the parentheses as the perfect square we've created:
Rewriting the left side as a subtraction we have:
And we have the proper form. We can see that the vertex is (10, 100). And so, like our earlier solution, x = 10 and (20-x) = 10 are the two positive integers that add up to 20 and provide the largest possible product (100).
|
|
|
