Question 238218: i really need this answer
and the steps to it
log(base 3)(x^2-3) is greater than 0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a couple of solutions:- This solutions is based mostly on logic and and understanding of exponents and logarithms.
- It takes time to get used to what logarithms represent. Your logarithm,
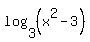 , represents "the exponent for 3 which results in , represents "the exponent for 3 which results in  . . - The equation says this exponent is greater than zero.
- Now let's think about exponents. A zero exponent results in a 1. Exponents greater than zero result in numbers greater than 1. And exponents less than 0 (negative) result in numbers between 0 and 1.
- Putting all this together, since the logarithm (i.e. the exponent for 3) is greater than 0, the result,
 , will be greater than 1: , will be greater than 1:

- Now we have an inequality (without logarithms) to solve. (See the conclusion for its solution.)
- This solution is based on rewriting the equation in exponential form. It may seem shorter and easier. But even I was unsure initially how to do this correctly with the inequality. Rewriting
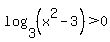 in exponential form gives us in exponential form gives us 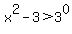 . Since . Since  we get: we get:  which is the same inequality we got above. which is the same inequality we got above.
Solving 
This is a quadratic inequality and these can be difficult if you haven't done many. Here's how I solve them. Get one side equal to 0:

Factor
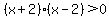
So far the steps have been the same ones we would use for an equation. But now, because it is an inequality, we will not be able to use the Quadratic Formula or the Zero Product Property as we would with an equation. What we have is a product that is greater than zero. Another way of putting this is that the product is positive. And how do we end up with positive results when multiplying two numbers? Answer: When they are both positive or both negative. This will be the basis of the next step. We will write inequalities which describe "both factors are positive or both factors are negative".
We could use:
(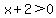 and and 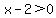 ) or ( ) or ( and and 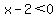 ). ).
But we can use something simpler if we use the following logic:- If the smaller of two numbers is positive, the larger number would have to be positive, too.
- If the larger of two numbers is negative, the smaller number would have to be negative, too.
- No matter what number x may be, x-2 will be smaller than x+2.
With this logic we can use:
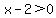 or or 
The first one says "the smaller factor is positive" (which makes both factors positive) and the second says "the larger factor is negative" (which make both factors negative). This pair is much easier to solve than the 4 used earlier. Solving these we get:
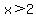 or or 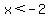
We can and should check these answers. We have to make sure we do not get negatives or zeros in the argument of any logarithms. These answers check out. Even 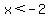 works because in the argument of the logarithm x gets squared. works because in the argument of the logarithm x gets squared.
|
|
|