Question 238159: The volume of a box is 32m^3, to reduce cost the box is to have minimum surface area. It is a square box with no top. What dimensions(height, length, width) should the box have?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume of a box is 32m^3, to reduce cost the box is to have minimum surface area. It is a square box with no top.
What dimensions(height, length, width) should the box have?
:
If it is square, they would all dimensions have to be the same, right?
:
Let x = the sides and height of the square box
:
x^3 = 32
x =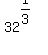
x ~ 3.1748 meters
:
If just the bottom is square, the height can be determined for minimum surface area. If that is what you mean, let me know and we can calculate that.
|
|
|