|
Question 237865: Need help factoring this problem completely (hint we are suppose to use grouping)
8x^2+10-4x^2y-5y
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!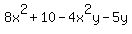 
To factor by grouping it is often a good idea to start by rewriting the expression as all additions. Having the expression as all additions allows the use of the Commutative and Associative Properties, if needed, to rearrange the order of the terms and to group them. So your expression, written with additions is:
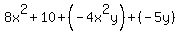
Now we can start factoring. When factoring by grouping we look for groups, usually pairs, of terms that have a common factor between them. (This may require reording and regrouping the terms which is why we changed to additions.) In your expression the first two terms have 2 as a common factor and the last two terms have y as a common factor. So we can factor these out of each pair:
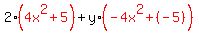
Now, if we're lucky the "other" factors (in red) in each group will match. Yours do not match. But they are the negatives of each other! Since they are negatives of each other, we can factor out a -1 from one of them and then they will match:
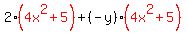
Now they match!!. (Note: If these factors do not match, even after factoring out -1 like we have, then we would have to start all over, reorder and rearrange into different pairs, and try again. And remember that not all expressions will factor using this method so there may be no reordering that works.)
Now we factor out these matching factors from each group:
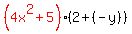
Note where the terms of the second factor come from (the black parts of the previous expression).
Now that the entire original expression is a product of two expressions, we have successfully factored the expression.
This may not look like we're finished. The reason for this is that factoring is a means to an end, not an end itself. The purpose of this problem is to get you to practice and get better at factoring. Here's some example problems where factoring 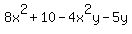accomplishes something:- Solve
 . We would solve this by factoring it:
and then using the zero product property which says that this (or any) product is zero only if one of the factors is zero:
 or 
The first equation has no solution but the solution to the econd equation is y = 2. So x can be any number and, as long as y = 2, the equation will be true. - Reduce the fraction
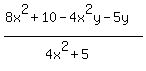 . Reducing fractions involves canceling common factors so we need to factor:
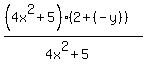
Now we can cancel the common factor:
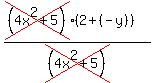
leaving
|
|
|
| |
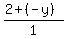
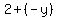
