SOLUTION: Find the reference angles "theta" or ϴ for the angles given below. Find the quadrants in which the angles lie. In addition, show all the steps for deriving the answer. 1.

The upper right hand quarter of the graph is QI (the first
quadrant)
The upper left hand quarter of the graph is QII (the second
quadrant)
The lower left hand quarter of the graph is QIII (the third
quadrant)
The lower right hand quarter of the graph is QIV (the fourth
quadrant)

The actual angle ϴ is the angle of rotation beginning
at the right hand side of the x-axis (the initial side)
and swinging counter-clockwise around to the terminal side
when the measure of the actual angle ϴ is positive, and 
swinging clockwise around to the terminal side when the
measure of the actual angle ϴ is negative. 

The reference angle of ϴ is the nearest angle taken 
positive, to the x-axis.

In each case below the blue arc represents the actual 
angle ϴ, and the green arc represents the reference angle.

Here ϴ is in QI and its reference angle is also 50°.

Here ϴ is in QII and its reference angle is 60°, gotten
by subtracting 120° from 180°.

This is in radians and is a special angle.  We change to 
degrees by multiplying by .





Here ϴ is in QIII and its reference angle in radians
is , gotten by subtracting  from  
like this:

This is also in radians, but it is not a special
angle.  It is a little more than 
radians, which is a little more than 180°.  So
we draw the angle a little into QIII:


 
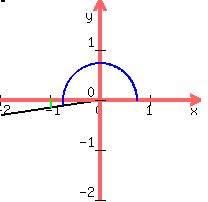Here ϴ is in QIII and the reference angle is 
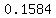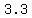gotten by subtracting  from  like this:

Here ϴ is in QIV and its reference angle is 60°, gotten
by subtracting 300° from 360°.

This is a negative angle so it swings clockwise from
the right side of the x-axis like this:



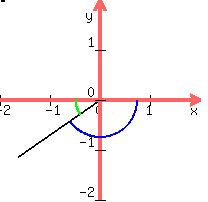Here ϴ is in QIII and its reference angle is 35°, gotten
by subtracting 145° from 180°.

Edwin