use descartes rule of signs to determine the possible number of positive real zeros and negative zeros. 
List all the terms of  Term #1.
Term #1. 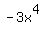 . Therefore, term #1 has a NEGATIVE sign
Term #2.
. Therefore, term #1 has a NEGATIVE sign
Term #2. 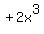 . Therefore, term #2 has a POSITIVE sign
Therefore in going from Term #1 to Term #2 there was a change in
sign, from negative to positive. So far that's 1 sign change.
Term #3.
. Therefore, term #2 has a POSITIVE sign
Therefore in going from Term #1 to Term #2 there was a change in
sign, from negative to positive. So far that's 1 sign change.
Term #3. 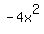 Therefore, term #2 has a NEGATIVE sign
Therefore in going from Term #2 to Term #3 there was another change
in sign, from positive to negative. So far that's 2 sign changes.
Term #4.
Therefore, term #2 has a NEGATIVE sign
Therefore in going from Term #2 to Term #3 there was another change
in sign, from positive to negative. So far that's 2 sign changes.
Term #4.  . Therefore, term #2 has a POSITIVE sign
Therefore in going from Term #3 to Term #4 there was another change in
sign, from negative to positive. So far that's 3 sign change.
Term #5.
. Therefore, term #2 has a POSITIVE sign
Therefore in going from Term #3 to Term #4 there was another change in
sign, from negative to positive. So far that's 3 sign change.
Term #5.  . Therefore, term #5 has a NEGATIVE sign
Therefore in going from Term #4 to Term #5 there was another change
in sign, from positive to negative. So far that's 4 sign changes.
So the fact that there are 4 sign changes means that the maximum number of
positive zeros is 4. But since complex imaginary zeros come in pairs,
There may be only 2 positive zeros, (in case there happens to be one pair
of complex imaginary zeros). Also there may be 0 positive zeros, (in case
there happens to be two pairs of complex imaginary zeros).
So there are either 4 or 2 or 0 positive 0's.
Now the number negative zeros of
. Therefore, term #5 has a NEGATIVE sign
Therefore in going from Term #4 to Term #5 there was another change
in sign, from positive to negative. So far that's 4 sign changes.
So the fact that there are 4 sign changes means that the maximum number of
positive zeros is 4. But since complex imaginary zeros come in pairs,
There may be only 2 positive zeros, (in case there happens to be one pair
of complex imaginary zeros). Also there may be 0 positive zeros, (in case
there happens to be two pairs of complex imaginary zeros).
So there are either 4 or 2 or 0 positive 0's.
Now the number negative zeros of  will be the number of
positive zeros of
will be the number of
positive zeros of 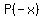 So let's substitute
So let's substitute  for
for  in
in  to get
to get
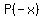
 Simplify:
Simplify:
 List all the terms of
List all the terms of 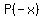 Term #1.
Term #1. 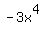 . Therefore Term #1 has a NEGATIVE sign.
Term #2.
. Therefore Term #1 has a NEGATIVE sign.
Term #2. 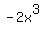 . Therefore Term #2 also has a NEGATIVE sign.
Therefore there is no sign change from Term #1 to Term #2. So far 0 sign changes.
Term #3.
. Therefore Term #2 also has a NEGATIVE sign.
Therefore there is no sign change from Term #1 to Term #2. So far 0 sign changes.
Term #3.  . Therefore Term #3 also has a NEGATIVE sign.
Therefore there is no sign change from Term #2 to Term #3. So far there
are still 0 sign changes.
Term #4.
. Therefore Term #3 also has a NEGATIVE sign.
Therefore there is no sign change from Term #2 to Term #3. So far there
are still 0 sign changes.
Term #4.  . Therefore Term #4 also has a NEGATIVE sign.
Therefore there is no sign change from Term #3 to Term #4. So far there
are still 0 sign changes.
Term #5.
. Therefore Term #4 also has a NEGATIVE sign.
Therefore there is no sign change from Term #3 to Term #4. So far there
are still 0 sign changes.
Term #5.  . Therefore Term #5 also has a NEGATIVE sign.
Therefore there is no sign change from Term #4 to Term #5. So far there
are still 0 sign changes.
So there are 0 positive zeros of
. Therefore Term #5 also has a NEGATIVE sign.
Therefore there is no sign change from Term #4 to Term #5. So far there
are still 0 sign changes.
So there are 0 positive zeros of 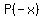 and therefore there are
0 negative zeros of P(x).
Answer: P(x) has 4 or 2 or 0 POSITIVE zeros and 0 NEGATIVE zeros.
[By doing further study on P(x), which you will eventually learn to
do, we could discover that P(x) actually has 0 real zeros, and 2 pairs
of complex imaginary zeros.]
Edwin
and therefore there are
0 negative zeros of P(x).
Answer: P(x) has 4 or 2 or 0 POSITIVE zeros and 0 NEGATIVE zeros.
[By doing further study on P(x), which you will eventually learn to
do, we could discover that P(x) actually has 0 real zeros, and 2 pairs
of complex imaginary zeros.]
Edwin