SOLUTION: a variable electric voltage in a circuit is given by the equation below, where t is the time (in s). If the voltage is on for 7s, when is V=0? V = t^4 - 19t^3 + 133t^2 - 405t + 45

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: a variable electric voltage in a circuit is given by the equation below, where t is the time (in s). If the voltage is on for 7s, when is V=0? V = t^4 - 19t^3 + 133t^2 - 405t + 45      Log On


   

Question 236629: a variable electric voltage in a circuit is given by the equation below, where t is the time (in s). If the voltage is on for 7s, when is V=0?
V = t^4 - 19t^3 + 133t^2 - 405t + 450
Looking for three answers in seconds.
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
V+=+t%5E4+-+19t%5E3+%2B+133t%5E2+-+405t+%2B+450
If the voltage is on for 7s...
I'm assuming that there are two parts to this problem. One is to find the voltage at 7 seconds and the other to find the time(s) when the voltage is zero.

For the first part, one can replace t with seven and figure out the voltage. But it is easier, IMHO, to use Synthetic division:
7 |  1  -19  133  -405  450
---       7  -84   343 -434
    ------------------------
     1  -12   49   -62   16

The voltage at 7 seconds is 16.

Finding when the voltage is zero is more difficult. We have to solve:
0+=+t%5E4+-+19t%5E3+%2B+133t%5E2+-+405t+%2B+450
And the only way to solve this is to factor it. And it does not factor easily. There is no Greatest Common Factor (other than 1), it does not fit any of the factoring patterns and it is not a trinomial. The only factoring methods left to us, then, are factoring by grouping and factoring by trial and error of the possible rational roots. With five terms factoring by grouping, if it is possible at all, will be challenging. So I'll try the possible rational roots.

There are many factors of 450 so there are many possible rational roots. Fortunately we can exclude any negative roots. This is so because the terms with even exponents are always positive. So the only way to get zero is to cancel out these positive terms with negative values coming from the terms with odd exponents. Since the terms with odd exponents all have negative signs in front of them we need the x's to be positive. We'll use Synthetic Division to test the possible roots:
2 |  1  -19  133  -405  450
---       2  -34   198 -414
    ------------------------
     1  -17   99  -207   36
So 2 is not a root

3 |  1  -19  133  -405  450
---       3  -48   255  450
    ------------------------
     1  -16   85  -150    0
3 is a root!

So t%5E4+-+19t%5E3+%2B+133t%5E2+-+405t+%2B+450+=+%28t-3%29%28t%5E3+-+16t%5E2+%2B85t+-150%29. We will now continue to factor by looking for roots of 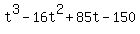t%5E3+-+16t%5E2+%2B85t+-150:
Try 3 again
3 |  1  -16   85  -150
---       3  -39   138
    ------------------
     1  -13   46   -12
3 is not a root a second time.

5 |  1  -16   85  -150
---       5  -55   150
    ------------------
     1  -11   30     0
5 is  root!

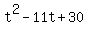So t%5E4+-+19t%5E3+%2B+133t%5E2+-+405t+%2B+450+=+%28t-3%29%28t-5%29%28t%5E2+-+11t+%2B+30%29. Since t%5E2+-+11t+%2B+30 is a trinomial we can factor this as a trinomial giving:

Now our equation is
0+=+%28t-3%29%28t-5%29%5E2%28t-6%29
and since it is factored we can solve it. The only way for this product to be zero is if one or more of the factors is zero. So
t-3+=+0 or t-5+=+0 or t-6+=+0
Solving these we get
t+=+3 or t+=+5 or t+=+6
So at times 3, 5 and 6 seconds the voltage is 0.

Since (t-5) was a factor twice is counts as two roots. It is a double root (or a root of multiplicity of two). So we have the four roots a 4th degree equation should have: 3, 5 (twice) and 6.