SOLUTION: 4x^4+4 divided by x^3+14x Find the Vertical, Horizontal and Oblique asymptotes

Algebra ->  Rational-functions -> SOLUTION: 4x^4+4 divided by x^3+14x Find the Vertical, Horizontal and Oblique asymptotes      Log On


   

Question 236572: 4x^4+4 divided by x^3+14x
Find the Vertical, Horizontal and Oblique asymptotes
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!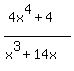
%284x%5E4%2B4%29%2F%28x%5E3%2B14x%29
Vertical Asymptotes. Vertical asymptotes occur for x values that make the denominator of the (simplified) fraction zero. (The fraction should be reduced/simplified, if possible, before determining the vertical asymptotes.) So we start by factoring the numerator and denominator:
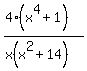
%284%28x%5E4+%2B+1%29%29%2F%28x%28x%5E2+%2B+14%29%29
This is all the factoring that can be done. And, as we can see, there are no common factors to cancel. So we now determine what values for x will make the denominator zero. Having the denominator factored helps in this. The only way 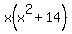x%28x%5E2%2B14%29 can be zero is if one (or more) of the factors is zero. So
x+=+0 or x%5E2%2B14+=+0
With some thought we should be able to realize that 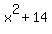x%5E2+%2B+14 can never be zero! x%5E2 would have to be -14. But the square of no real numbers would be negative. Therefore the only x value that makes the denoimnator zero is zero itself. We have one vertical asymptote: x=0 (which is the y-axis).

Horizontal and Oblique Asymptotes. These asymptotes, if any, occur for very large positive and/or negative values for x. To find them we need to be able to analyze the function for these large values of x. So we will use some Algebra on the function to transform it into a form which we can better determine what happens for large values of x. The steps of this transformation are these:
  1. If the degree of the numerator is equal to or greater than the degree of the denominator, then use long division to divide the fraction.
  2. At this point, the only fraction (with x in the denominator) that remains should have a numerator whose degree is less than the degree of the denominator. multiply the numerator and denominator of this fraction by the reciprocal of the largest power of x in the fraction.

Let's try this on your function.
1. Divide if the degree of the numerator is greater than or equal to the degree of the denominator. The degrees of your numerator and denominator are 4 and 3 respectively. So we need to divide, using long division:
         4x
         ____________________________
x^3+14x /4x^4 + 0x^3 +  0x^2 + 0x + 4
         4x^4 +      + 56x^2
         -------------------
                      -56x^2      + 4

So %284x%5E4%2B4%29%2F%28x%5E3%2B14x%29+=+4x+%2B+%28-56x%5E2+%2B+4%29%2F%28x%5E3+%2B+14x%29
2. Multiply the numerator and denominator of the fraction by the reciprocal of the largest power of x in the fraction. The largest power of x in this fraction is x%5E3 so we'll multiply by 1%2Fx%5E3"


Now we have a form we can analyze to see what happens when x becomes a very large number. Look at all the "little" fractions within the big fraction. As x becomes a very large number, these "little" fractions become very small. The larger x gets the smaller these "little" fractions get. In fact these "little" fractions will become very close to zero in value. So we can, in effect, treast these "little" fractions as if they were zero. So when very large values of x, our transformed function becomes, in effect:

So the oblique asymptote is: y = 4x. (It is oblique because y = 4x in not horizontal.)

Additional note: The procedure I've given you will also find asymptotes which are not even lines!