divide the polynomials using long divisin. What is Q(x) and r(x)?
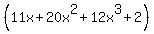 by
by 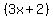
(elevenx+twentyx to the second power+ twelvex to the third power + two) divided by (threex+2)
First write the polynomial in descending order of powers of x
12x³ + 20x² + 11x + 2
Then write
_______________________
3x + 2) 12x³ + 20x² + 11x + 2
Divide the first term 12x³ by 3x:  and write 4x² above the 20x²:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
Multiply the 4x² by the (3x + 2) getting
and write 4x² above the 20x²:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
Multiply the 4x² by the (3x + 2) getting  and
write it under the first two terms and draw a line underneath:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
Subtract
and
write it under the first two terms and draw a line underneath:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
Subtract  ,
and write 12x² under the line under 8x², like this:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x²
Now bring down the next term + llx and write in next to the 12x²
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
Divide the first term on the bottom 12x² by 3x:
,
and write 12x² under the line under 8x², like this:
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x²
Now bring down the next term + llx and write in next to the 12x²
4x²__________
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
Divide the first term on the bottom 12x² by 3x:  and write + 4x above the 11x at the top, like this:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
Multiply the 4x by the (3x + 2) getting
and write + 4x above the 11x at the top, like this:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
Multiply the 4x by the (3x + 2) getting  and
write it under the first two terms and draw a line underneath:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
Subtract
and
write it under the first two terms and draw a line underneath:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
Subtract  ,
and write 3x under the line under 8x, like this:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x
Now bring down the last term + 2 and write in next to the 3x
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
Divide the first term on the bottom 3x by the 3x at the left:
,
and write 3x under the line under 8x, like this:
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x
Now bring down the last term + 2 and write in next to the 3x
4x² + 4x____
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
Divide the first term on the bottom 3x by the 3x at the left:
 and write + 1 above the + 2 at the top,
like this:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
Multiply the + 1 by the (3x + 2) getting
and write + 1 above the + 2 at the top,
like this:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
Multiply the + 1 by the (3x + 2) getting  and
write it under the two terms at the bottom and draw a line
underneath:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
3x + 2
Subtract
and
write it under the two terms at the bottom and draw a line
underneath:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
3x + 2
Subtract  ,
and write 0 under the line under 2, like this:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
3x + 2
0
Now you are done and the answer is
,
and write 0 under the line under 2, like this:
4x² + 4x + 1
3x + 2) 12x³ + 20x² + 11x + 2
12x³ + 8x²
12x² + 11x
12x² + 8x
3x + 2
3x + 2
0
Now you are done and the answer is 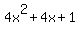 and
since the remainder is 0 you do not have to put it over
the divisor
and
since the remainder is 0 you do not have to put it over
the divisor 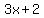 and add it on like you do when
the remainder is not 0.
Edwin
and add it on like you do when
the remainder is not 0.
Edwin