SOLVE EACH EQUATION, WHERE 0 DEGREES (< OR = TO) X < 360 DEGREES. ROUND APPROXIMATE SOLUTIONS TO THE NEAREST TENTH OF A DEGREE 3 SIN X - 5 + CSC X = 0
 Change
Change 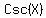 to
to 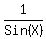
 Multiply through by
Multiply through by 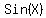 to clear of fractions:
to clear of fractions:



 Use the quadratic formula:
where
Use the quadratic formula:
where  ,
,  ,
,  , and
, and 



 Using the +
Using the +
 That's impossible because all sines are between -1 and +1.
Using the -
That's impossible because all sines are between -1 and +1.
Using the -
 That is a positive number and is between -1 and +1,
so that will give us two solutions, since the sine
is positive in quadrant I and quadrant II.
To find the quadrant I solution, we find the
inverse sine of 0.2324081208 which is
13.56526739° which rounds to 13.6° to the nearest
tenth of a degree.
That's the reference angle, and in Quadrant I, the
solution IS the reference angle, 13.6°
To find the quadrant II solution, we subtract the
reference angle, 13.6° from 180° and get 166.4°
So the two solutions are X = 13.6° and X = 166.4°.
Edwin
That is a positive number and is between -1 and +1,
so that will give us two solutions, since the sine
is positive in quadrant I and quadrant II.
To find the quadrant I solution, we find the
inverse sine of 0.2324081208 which is
13.56526739° which rounds to 13.6° to the nearest
tenth of a degree.
That's the reference angle, and in Quadrant I, the
solution IS the reference angle, 13.6°
To find the quadrant II solution, we subtract the
reference angle, 13.6° from 180° and get 166.4°
So the two solutions are X = 13.6° and X = 166.4°.
Edwin