Question 23382: Solve the rational inequality. State and graph the solution set. Can someone help?
x/x+2>-1
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! I'm assuming that you mean  .
If so, then I would begin by setting the inequality to zero. DO NOT MULTIPLY BOTH SIDES OF THE INEQUALITY BY (X+2)!!
 .
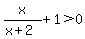Next, find a common denominator, which is x+2:
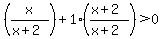
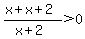
Now, you have two choices for method of solving the inequality. You can use some algebra explanations to solve it, or you can use a graphing calculator (or the algebra.com calculator!!). I will choose the latter method. You need to graph  . Before drawing the graph, notice that there is one place that the numerator equals zero, and that is at x= -1. There is one value of x that would make the denominator zero, which is NOT allowed, and that would be x= -2. This tells me that there is a ROOT at x = -1 and an ASYMPTOTE at x= -2. Now, draw the graph with this in mind:
Now, since the problem is to solve , which is solving a problem that is "GREATER THAN", you need to find all values of x for which the graph is ABOVE the x-axis. And do NOT include the endpoints.
Notice that the graph is above the x-axis from -infinity to -2, and also from -1 to infinity.
This means that the solution is x<-2 or x>1.
In interval notation this will be:(-inf, -2) U (-1, inf).
R^2 at SCC
|
|
|
