Question 233451: steve McPoke left home on his bivcycle at 8 am. traveling at 18 km/h. at 10 am, steve's brother set out after him on a motorcycle , folowing the same route. The motorcycle traveled at 54 km/h. How long had steve traveled when his brother overtok him?
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's start with the distance formula:
 where d = distance traveled, r = rate (speed), and t = time of travel. We can write two such equations, one for Steve (1) and the other for his brother (2): where d = distance traveled, r = rate (speed), and t = time of travel. We can write two such equations, one for Steve (1) and the other for his brother (2):
 and... and...

Now when Steve's brother on the motor bike overtakes Steve on his bicycle, each will have traveled the same distance, so:
 and, since Steve's brother set out two hours after Steve did (10 am - 8 am), then Steve's time is two hours more than his brother's time, and, of course, the speeds of both are given, so: and, since Steve's brother set out two hours after Steve did (10 am - 8 am), then Steve's time is two hours more than his brother's time, and, of course, the speeds of both are given, so:
 Now we have enough information to complete the two equations: Now we have enough information to complete the two equations:

 Since Since  we'll set these two equations equal to each other to get: we'll set these two equations equal to each other to get:
 Solve for Solve for 
 Subtract Subtract 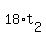 from both sides. from both sides.
 Divide both sides by 36. Divide both sides by 36.
 but we want Steve's time ( but we want Steve's time ( , so... , so...
 Substitute Substitute 


Steved had traveled for 3 hours when his brother overtook him.
|
|
|