|
Question 233253: How do I factor: x^3-9x^2-16x+144
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! There is a wide variety of techniques for factoring including GCF, patterns, trinomials, factoring by grouping and trial and error of possible rational roots. When factoring expressions you must be ready to use any and all of these techniques. The only "rule" is to start with Greatest Common Factor (GCF) factoring. After that you use any appropriate techniques, perhaps repeatedly, until you can factor no more.
With your expression, the GCF is 1 and there is rarely any reason to factor out a 1. Your expression has 4 terms. None of the patterns have 4 terms and trinomials are 3 term expressions. So we are left with factoring by grouping and trial and error. As the name implies, trial and error involves trials which may fail. So we'll try factoring by grouping before we resort to trial and error.
To factor by grouping, I recommend that you rewrite the expression as all additions so that you have to option of using the Commutative and Associative Properties to reorder and regroup the terms in any way you choose. So your expression now looks like:
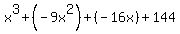
Now we look for groups of terms, usually pairs, which can be factored, usually with a GCF. (This is a GCF for just the subexpression. Any GCF for the entire expression should already be factored out by now.) Since the first two terms have a GCF of  and since the last two terms have a GCF of 16, we do not need to rearrange the terms to get started. We just factor the GCF out of each pair of terms giving us:
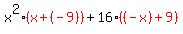
If we are lucky, the "other" factors (the ones in red above) in each pair will match. These do not match. But they are opposites/negative of each other! So we are not totally out of luck. We can factor out a -1 from one pair and make them match. (Factoring out a -1 can always be done and it helps to keep you eyes out for when doing so helps solve a problem.) Factoring out a -1 from the second group:
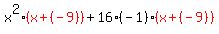
or
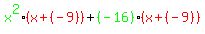
Now our "other" factors match and we can proceed. (In other problems, if you are unable to match these factors, try starting over and trying a different grouping of terms.) Now we factor out the common factor (red) from each group. (Note where the parts in green come from and go:
It is tempting, after succeeding up to this point, to feel satisfaction and stop. But always factor until you cannot factor any further. And the second factor above (in green) is a difference of squares and will factor according to the pattern:  . In this expression the "a" is "x" and the "b" is "4". Factoring the second factor accorsing to the pattern gives us:
And, since nothing else will factor no matter what technique we try to use, we are finished!
|
|
|
| |
