Question 23238: Help with graphing questions. Thank you so much
Write down the equations of the line described in the following equations:
1. The line passes through the points (8,2) and (4,-7)
2. The line passes through the point (4,4) and has a slope of -4
3. The line has a y-intercept of 5 and a slope of 3.
4. The line has a x-intercept of 5 and a slope of 3
Answer by philberg99(10)   (Show Source): (Show Source):
You can put this solution on YOUR website! Anytime you have a line, you need three formulas:
Formula 1: slope: m = 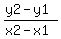
Formula 2: point slope form: y - y1 = m(x-x1)
Formula 3: slope intercept form: y = mx + b
(x1,y1) and (x2,y2) are two points on your line, m is the slope, and b is the y intercept.
So for your first problem, the two points we're looking at are (8,2) and (4,-7). Using the first formula, m = 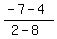 = =  = = 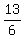 . Now we use the second formula to get the line you want. The equation for the line will be y - 2 = . Now we use the second formula to get the line you want. The equation for the line will be y - 2 = 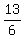 (x-8). If you want it in y = mx+b form, add two to both sides and distribute the (x-8). If you want it in y = mx+b form, add two to both sides and distribute the 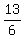 to get y = to get y = 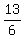 x - x - 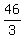 . .
For the second one, the first formula can be skipped since we already know the slope. So the equation becomes y - 4 = -4(x-4). Again if you want the y = mx+b form, solve for y to get y = -4x + 20.
For the third one, using the third formula gives us that the line is y = 3x + 5.
The fourth one requires a little work. Using the third formula, we have that y = 3x + b, where b is the y intercept. But we do not know the y intercept in this case so we don't know b just yet. However we do know that the x intercept is 5. This means that if we plug zero in for y, then we should get an x value of 5. So using this, we have 0 = 3*(5) + b, so 0 = 15 + b, and thus b = -15. Therefore our line is y = 3x - 15.
|
|
|