|
Question 232378: Factor completely
28x^2 -29x + 6/-28x^2 + 50x -12
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Whenever you factor, always start by factoring out the Greatest Common Factor (GCF), unless it is a 1. In the denominator the GCF is 2:
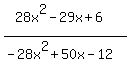
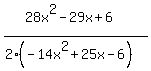
Since negative leading coefficients complicate things, I'm going to factor out a -1 in the denominator:
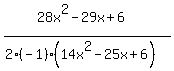
Now we have a couple of trinomials to factor, if possible. Factoring trinomials with a leading coefficient of 1 is fairly easy. When the leading coefficients are not 1's, the factoring can involve a lot of trial and error. With leading coefficients of 28 amd -14, you trinomials are of the second kind.
To factor these types of trinomials we are looking for a certain combination of factors of the leading coefficient and factors of the constant term. If the trinomial factors, it will look like:
(px+q)(rx+s)
where p and q are factors of the leading coefficient and r and s are factors of the constant term. Often there may be many possible factors of the leading coefficient and/or constant term (and you should also consider the negatives of the factors of the constant term. The right p, q, r and s will fit the following equation:
ps + qr = b
where b is the coefficient of the middle term of the trinomial. Note: there is only one right combination!
To factor the numerator we are looking for factors of 28 (p and q) and factors of 6 (r and s) which fit ps + qr = -29. The factors of 28 are: 1 and 28, 2 and 14, and 4 and 7. The factors of 6 are 1 and 6, -1 and -6, 2 and 3, and -2 and -3. It takes some trial and error to find the right combination. (After doing several problems like this you get better at finding the right combination quickly.) After some effort we should find
(7x-2)(4x-3) works because 7*(-3) + (-2)(4) = -29
Note that we ended up needing the negatives of the factor of 6: -2 and -3.
Repeating this process on  we should find the right combination to be:
(7x-2)(2x-3) because 7(-3) + (-2)(2) = -25
Note that again we ended up needing the negatives of the factor of 6: -2 and -3.
So now our factored fraction looks like:
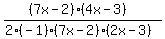
Now we can simplify by canceling common factors:
leaving:
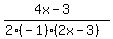
(NOTE: Nothing else cancels here. The x's, the -3's and the 4 and 2 are not factors and only factors cancel!)
All we can do at this point is to multiply out the denominator:
|
|
|
| |
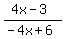
