Question 230782: Please help me solve these questions step by step.
(1). 3lnx+2lnx^2=6
(2). a*e^*x=k
(3). y=(3^2+4^2)^-1/2
(4). the number of people N(t) that buy particular product 1/2 days after a group of 1000 people. The product is given by N(t)=1000/1+999e^0.39t, how any people buy the product after 20 days, that is t=20
How many days does it take for 800 people to buy the product and will 1000 people ever buy the product, here calculate the t.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1). 
Solving problems like this, with the variable in the argument of a logarithm, is often done by transforming the equation into one of the following forms:
ln(variable-expression) = variable-less expression
or
ln(variable-expression) = ln(another expression)
In other words we want to condense the logarithms on each side of the equation into one logarithm and then isolate that logarithm. In order to condense multiple logarithms into one we need the following properties of logarithms:
The first two allow us to combine two logarithms into one. But they require that there are no coefficients in front of the logarithms. The third property allows us to "move" a coefficient into the argument of the logarithm.
Let's try these on your problem. First, we'll use the third property to "move" the coefficients on each of the logarithms:


Now we can use the first property above to combine the two logarithms:


We now have the equation in one of the desired forms. In this form you proceed by rewriting the equation in exponential form:

Now we find the 7th root of each side:



If you need a decimal approximation, you can use a calculator on this.
(2). 
Here we have an equation with the variable x in the exponent. In this situation we usually transform the equation into the form:
base^(variable expression) = expression
So we need to get rid of the a:

Now we have it in the proper form. At this point we will use logarithms to get the variable out of the exponent. Since the base is e, the natural (pardon the pun) is to use ln:

Now we can use the third property (see problem #1 above) in the other direction to "move" an exponent in the argument out in front:

Since the ln(e), by definition, is 1:

(3). 
All we have to do is simplify this one, following the order of operations (aka PEMDAS) of course:


A negative exponent means "reciprocal of" and 1/2 as an exponent means "square root of". The square root of 25 is 5 and the reciprocal of 5 is 1/5 so:

(4).  , how any people buy the product after 20 days, that is t=20 , how any people buy the product after 20 days, that is t=20
So you just substitute 20 in for t and reach for your calculator:






which makes me think the equation is incorrect. You'll have to fix the equation. Perhaps the exponent should be (-0.39t)?
I hope the solutions I have give here using the bad equation will still be helpful in finding the correct solutions to the correct equation.
How many days does it take for 800 people to buy the product
This time we have N and we want to find t:

This problem is similar to problem #2. We have a variable in an exponent we want to solve for. So we want to transform this into the form:
 = some expression = some expression
So we'll start by getting rid of the fraction by multiplying both sides by the denominator:

On the left we'll use the Distributive Property. On the right the denominator cancels out:


Subtract 800 from each side:

Divide by 799200:

Now we finally have the equation in the desired form. We will now find the ln of each side:


"move" the exponent out of the ln:

Since ln(e) = 1:

And last of all, divide by 0.39:

(Remember, the equation is incorrect so these answers, like negative time, do not make sense.)
... will 1000 people ever buy the product, here calculate the t.
With this equation:  the answer is no. The reasoning behind this answer is: the answer is no. The reasoning behind this answer is:- The only way
 can be equal to 1000 is if the denominator is 1 can be equal to 1000 is if the denominator is 1 - The only way the denominator,
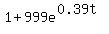 , can be 1 is if , can be 1 is if 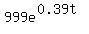 is zero. is zero. - The only way
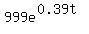 can be zero is if can be zero is if  is zero. is zero.  cannot ever be zero. e to any power (including the zero, fractional and negative exponents) is always a positive number. cannot ever be zero. e to any power (including the zero, fractional and negative exponents) is always a positive number.- So it is impossible for N(t) to be 1000.
Instead of this logic, you could also try to solve it like we did for N(t) = 800. But, after a lot of work, you'll find you have an equation with no solutions:


Divide by 1000:

Subtract 1:

We now have an equation which can be recognized as one with no solutions. By the Zero Product Property this product can be zero only if one of the factors is zero. 999 is never zero. And  also can never be zero no matter what t may be. So their product can never be zero.) Any work past this point is a waste of time. also can never be zero no matter what t may be. So their product can never be zero.) Any work past this point is a waste of time.
|
|
|