Question 229930: 3x-2y=-6 graph the equation
Answer by drj(1380)   (Show Source):
You can put this solution on YOUR website!  graph the equation
I'll show you two methods:
METHOD 1.
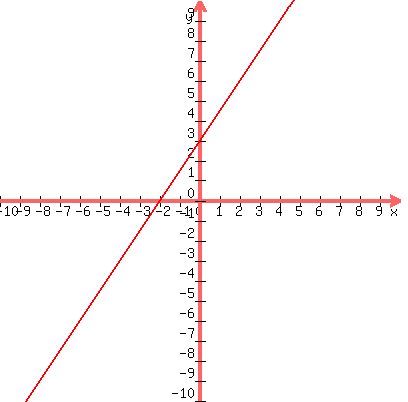
Step 1. It takes two points to make a line. Let's find these two points
Step 2. Let x=0, then 3*0-2*y=-6 or y=3. So we have (0,3) as one point.
Step 3. Let y=0, then 3x-2*0=-6 or x=-2. So we have (-2,0) as another point.
Step 4. Use these two points (0,3) and (-2,0) to draw the line.
METHOD 2
Step 1. Let's put the equation in slope-intercept form given as y=mx+b where m is the slope and b is the y-intercept when x=0 or at point(0,b).
Step 2. Putting in slope-intercept form yields the following steps.
Add 2y+6 to both sides of the equation
Divide 2 to both sides of the equation
 }
Step 3. ANSWER: The equation is where the slope m=3/2 and y-intercept b=3.
Need one more point to graph the line since we have (0,3) as one point. A slope m=3/2 means every move to two units to the right yields three steps upward.
So starting at (0,3) then one unit to the right means x2=0+2=2 and then two units down means y2=3+3=6. Then, the other point we can use to plot the line is (2,6). We can check if it satisfies the equation  or
 which it does.
Here's the graph:
I hope the above steps and explanation were helpful.
For Step-By-Step videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry please visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Also, good luck in your studies and contact me at john@e-liteworks.com for your future math needs.
Respectfully,
Dr J
http://www.FreedomUniversity.TV
|
|
|
