|
Question 229435: Find b2 - 4ac and the number of real solutions to each
equation. -3x2 + 7x = 0
The 2 next to the x is a to the power 2. I have no idea where to start for this problem how do I find b2 - ac, I do not understand anything it is saying in the readings either. Can someone please explain this to me in plain ole English???
Found 2 solutions by stanbon, Earlsdon:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find b^2 - 4ac and the number of real solutions to each
equation. -3x2 + 7x = 0
---------------------------------
A general quadratic form is ax^2 + bx + c = 0
---------------
Your Problem:
a = -3 ; b = 7 ; c = 0
---
So b^2 - 4ac = 7^2 - 4*-3*0 = 7^2 = 49
-------------------------------------------
Since b^2-4ac is positive the quadratic has two unequal Real Number solutions.
=========================================================================
Cheers,
Stan H.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have obviously started learning about quadratic equaions and their solutions.
The standard form of the quadratic equation is:
 in which the a, b, and c are positive or negative numbers and the a is not equal to zero. If the a were equal to zero then you wouldn't have a quadratic equation. in which the a, b, and c are positive or negative numbers and the a is not equal to zero. If the a were equal to zero then you wouldn't have a quadratic equation.
You can always find the solutions to a quadratic equation by using the "quadratic formula" which looks like this:

The a, b, and c in this formula correspond the a, b, and c in the standard form given above.
The part of the quadratic formula that lies under the square root sign ( ) is called the "discriminant". ) is called the "discriminant".
The value of the discriminant indicates the kind of roots (solutions) you can expect to find when you solve the quadratic equation.
If the value of the discriminant is positive, then the solution has two real roots.
If the value of the discriminant is negative, then the solution has two complex conjugate roots.
If the value of the discriminant is zero, then the soltion has one real root which is really two identical roots known as a double root.
In your quadratic equation:
 a = -3, b = 7, and c = 0 a = -3, b = 7, and c = 0
The solutions for this equation are given by:
 and here, the discriminant is: and here, the discriminant is:
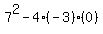 which evaluates to: which evaluates to:
 This is the value of This is the value of 
Since this is positive, the solution to your equation has two real roots.
Let's solve your equation using the quadratic formula: : :


 or or  and these can be simplified to: and these can be simplified to:
 or or  and these are the two real roots. and these are the two real roots.
|
|
|
| |