|
Question 229207: Rational Function:
y = (4x+6) / (x-2)
I need to know the X and Y Intercepts
All Asymptotes
Plots to graph to get the curves
Domain and Range
Increasing and Decreasing
And the Interval which the function is continuous
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Y-intercepts. Point(s) where a graph intersects the y-axis. Points on the y-axis have an x coordinate that is zero so to find y intercepts, make x zero and use the equation to figure out y:


So the y-intercept is (0, -3)
X-intercepts. Point(s) where a graph intersects the x-axis. Points on the x-axis have a y coordinate that is zero so to find x intercepts, make y zero and use the equation to figure out x:

The easiest way to solve this is to use the fact that a fraction, like the right side of the equation, is equal to zero only when the numerator is zero:



So the x-intercept is (-3/2, 0)
Vertical asymptotes. These occur for x values which make the denominator zero. But before we go looking for them, make sure the fraction is reduced first. To reduce a fraction we factor the numerator and denominator and cancel common factors, if any. Our numerator does factor so we should check to see if the fraction will reduce:

There are no common factors to cancel. Always check this first before finding vertical asymptotes. Now we can find the x-value(s) that make the denominator zero. We do this by setting the denominator to zero and solving:

 which is the vertical asymptote. which is the vertical asymptote.
(Note: Sometimes the fraction will reduce. The denominator may even disappear entirely! If this happens, there will be no vertical asymptotes.
Horizontal and Oblique Asymptotes. If they exist, they exist for large positive and/or negative values of x. To find them we analyze the equation to see what happens for very large positive or negative x values. This analysis is done by- If, when you looked for the vertical asymptotes, you were able to reduce the fraction, use that reduced fraction here, too.
- If the degree (highest exponent) of the numerator is greater than the degree of the numerator,
- Divide out the fraction
- Rewrite the equation in the form of: quotient + remainder/denominator
- Use this rewritten equation for the rest of the analysis.
Note: When you have a larger degree numerator than denominator, this is when you have oblique asymptotes. - Multiply the numerator and denominator by the reciprocal of the highest power of x present in the fraction.
- At this point your fraction may have little fractions in it. Any of the little fractions (with some power of x in the denominator) will approach zero for very large positive or negative values of x. So for very large x values, these little fractions, if any, will have no significant impact on the value of the overall fraction. So we can ignore them.
- The Horizontal or oblique asymptotes are the equations we get by ignoring the little fractions in the big fraction, if any.
Let's try this out on your equation:
1. Use the reduced fraction, if any. We were not able to reduce the fraction.
2. If the degree of the numerator is higher than that of the denominator, divide. In your equation the degrees are equal (since the highest exponent for x in both the numerator and denominator is 1).
3. Multiply by the reciprocal of the highest power of x. Our highest power is x is simply x. And the reciprocal of x is 1/x:

4. Ignore the little fractions, if any:

5. Our horizontal asymptote is: y = 4
The two intercepts and the two asymptotes are not much to go on when trying to graphing the equation. Some additional things we can do:- Create a table of values and plot some points. Some good x values for your table would use the value of x in the vertical asymptote as a "center". Use integers to the right and to the left of the vertical asymptote. In our case, since x = 2 is the vertical asymptote, try 3, 4, 5 and 1, (we already have x=0), -1
- Squeeze some more information from our work in finding the horizontal/oblique asymptotes. Look at the equation with the little fractions:

Think about this fraction for very large x values:- Large positive x's:
- 6/x is a very tiny positive fraction so the numerator will be a tiny bit larger than 4.
- 2/x is a very tiny positive fraction so the denominator will be a tiny bit less than 1 (since we're subtracting the 2/x).
- The fraction as a whole would be (a tiny bit more than 4)/(a tiny bit less than 1. As a whole fraction the would work out to be a tiny bit more than 4.
So when is is large positive numbers, y will be a little bit more than 4. This means the graph will approach y = 4 from above.
- Large negative x's:
- 6/x is a very tiny negative fraction so the numerator will be a tiny bit less than 4.
- 2/x is a very tiny negative fraction so the denominator will be a tiny bit more than 1 (since we're subtracting the tiny negative fraction, 2/x).
- The fraction as a whole would be (a tiny bit less than 4)/(a tiny bit more than 1. As a whole the fraction would work out to be a tiny bit less than 4.
So when is is large negative numbers, y will be a little bit less than 4. This means the graph will approach y = 4 from below.
Now we're ready to attempt a graph:- Draw your asymptotes as dotted lines.
- Plot your points:
- The intercepts
- The points from your table of values
- Try to "connect the dots" using a smooth curve. If you don't think you have enough, expand your table of values and plot these additional points.
- Your graph must not cross your vertical asymptote(s)!! (The horizontal/oblique asymptotes may be crossed for x values which are not extremely large.)
Your graph should look something like:

(Note: Algebra.com's graphing software is weak on asymptotes. Rather than having incomplete and incorrectly drawn asymptotes, I've left them out.)
Domain: All real numbers except those which make the denominator zero. So for your equation, the domain is all real numbers except 2.
Range: The only possible number we might suspect that y could never be is 4 because y=4 is our horizontal asymptote. But we can tell if y could be 4 by setting it to four and solving for x:

Multiply both sides by (x-2):

Subtract 4x from each side:

As we can see, there is no solution. So y cannot ever be 4. So our range is all Real numbers except 4.
Increasing/decreasing. This can be done visually from the graph or by use of Calculus. I'll leave this up to you.
Intervals of continuity. Any x values which make the original denominator zero will be points where the function is not continuous. we have only one such value: x=2. So the intervals of continuity would be:
(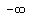 , ,  ) and ( ) and ( , ,  ) )
One final note. Sometimes there are x values which make the original denominator zero but not the reduced denominator zero. For these x values, if any- the function will not be continuous.
- there will not be a vertical asymptote. Instead there will be a "hole" in the graph at that point.
Here's an example:

x = -3 will make this denominator zero.
If we reduce the fraction:

Our reduced equation is y = x which has no denominator. So there there is no vertical asymptote at -3. The graph of  will be, therefore, exactly the same as the graph of y=x (which is a line) except there will be a "hole" in the line at x = -3! will be, therefore, exactly the same as the graph of y=x (which is a line) except there will be a "hole" in the line at x = -3!
|
|
|
| |