|
Question 227505: what do u do to this funtion find f(g(x))and g(f(x))
f(x)x 2 power -1 g(x)= 1/x-1
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Working with functions becomes much easier if you get a better grasp of what the function rule means and what the role of "x" is in the function rule:- The function rule is more than a formula. It is a description, in the language of Mathematics, of how the function works. It describes what the particular function will do with its input in order to come up with its output.
- The role of the "x" in the function rule is as a place-holder. In the parentheses on the left it represents whatever input is provided and on the right it represents whatever the function will do with the input.
Let's apply these ideas to your  . A literal reading of this: The function f squares x and then subtracts one. A better, more enlightened reading: The function f will take its input, whatever it is, squares it and then subtracts 1. If you give f a 10 as input, f will square it and then subtract 1. If you give f a "q", it will square it and then subtract 1. If you give it a 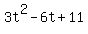 as input, f will square it and then subtract 1. No matter what you provide f as imput, f will square it and then subtract 1. This is what the function rule is really saying.
f(g(x)) means make g(x) the input to f. And what will f do?? It will square it and then subtract 1!!:
f(g(x)) = (g(x))^2 -1}}}
Substituting the function rule for g(x) we get:
f(g(x)) = ((1/x)-1)^2 - 1}}}
Your teacher probably wants this simplified. So using FOIL or the pattern  to multiply we get:
Now we can turn our attention to g(f(x)). This says make f(x) the input to the function g. The function g, as we can see from the rule:  , will find the reciprocal (1/x is the reciprocal of x) of the input and then subtract 1. So when you give it f(x), it will find the reciprocal of f(x) and then subtract 1:
Substituting the rule for f(x) we get:
This could be considered simplified enough. Or perhaps we should subtract (by getting common denominators first, of course):
Now we can subtract:
|
|
|
| |
