Question 226005: Torque left home on his bicycle at 9:00 A.M., traveling at an average rate of 12 mph. At noon, Torque's brother set out after him on a motorcycle, following the same route, averaging 39 mph. How long had Torque been riding when his brother caught up?
Will you help me set up the equation for this? i don't quite understand travel questions and I have a test in two days.
Thanks,
Emily M.
Ohio
Found 2 solutions by nerdybill, ankor@dixie-net.com:
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! Torque left home on his bicycle at 9:00 A.M., traveling at an average rate of 12 mph. At noon, Torque's brother set out after him on a motorcycle, following the same route, averaging 39 mph. How long had Torque been riding when his brother caught up?
.
You will need to apply the "distance formula"
d = rt
where
d is distance
r is rate or speed
t is time traveled
.
For his brother to catch up:
"distance Torque road on bicycle" = "distance his brother rode"
.
Let t = time Torque rode on his bicycle
then
t-3 = time his brother traveled on motorcylce
.
12t = 39(t-3)
12t = 39t-117
0 = 27t-117
117 = 27t
4.333 = t
Or
4 hours and 20 minutes
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! Torque left home on his bicycle at 9:00 A.M., traveling at an average rate of 12 mph.
At noon, Torque's brother set out after him on a motorcycle, following the same route, averaging 39 mph.
How long had Torque been riding when his brother caught up?
:
Let t = time Torque had been riding
then the brother starts, 3hrs later, therefore
(t-3) = travel time of the brother
:
A good fact to remember in these "catch up" problems, is when this occurs,
they both will have traveled the same distance
:
write a distance equation from this fact; (dist = speed * time)
:
bro dist = T's dist
39(t - 3) = 12t
39t - 117 = 12t
39t - 12t = +117
27t = 117
t =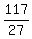 
t = 4 hrs (4 hr 20 min) is the riding time of T
;
:
Check the solution by finding the dist traveled by each
(bro traveled 4.33 - 3 = 1.33 hr)
4.33 * 12 ~ 52 mi
1.33 * 39 ~ 52 mi
|
|
|
