SOLUTION: Complete each of the following for the function g(x)=-3x^2-6x+1 a.Find the vertex of g(x) b.Find the x-intercept c.Find the y-intercept

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Complete each of the following for the function g(x)=-3x^2-6x+1 a.Find the vertex of g(x) b.Find the x-intercept c.Find the y-intercept       Log On


   

Question 224743: Complete each of the following for the function g(x)=-3x^2-6x+1
a.Find the vertex of g(x)
b.Find the x-intercept
c.Find the y-intercept
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Complete each of the following for the function g(x)=-3x^2-6x+1

a.Find the vertex of g(x)

b.Find the x-intercept

c.Find the y-intercept

g%28x%29=-3x%5E2-6x%2B1

Step 1. The general formula for a parabola is y-b=c%28x-a%29%5E2 where x=a and y=b is the vertex or at point (a,b). Here, c is a constant.

Step 2. Put g%28x%29=y=-3x%5E2-6x%2B1 in standard form by completing the square in x with the following steps.

y=-3x%5E2-6x%2B1=-3x%5E2-6x-3%2B3%2B1=3%28x%2B1%29%2B4 where we added zero 0=-3+3 to complete the square

Factor out -3 in the first three terms

y=-3%28x%5E2%2B2x%2B1%29%2B3%2B1=-3%28x%2B1%29%5E2%2B4

Subtract 4 from both sides of the equation


y-4=-3%28x%2B1%29%5E2%2B4-4

y-4=-3%28x%2B1%29%5E2

ANSWER: So the vertex is located at point (-1, 4)


Step 3. To find the x-intercept, set g(x)=y=0. We use the quadratic formula given as

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=-3, b=-6 and c=1

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -3x%5E2%2B-6x%2B1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-6%29%5E2-4%2A-3%2A1=48.

Discriminant d=48 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--6%2B-sqrt%28+48+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-6%29%2Bsqrt%28+48+%29%29%2F2%5C-3+=+-2.15470053837925
x%5B2%5D+=+%28-%28-6%29-sqrt%28+48+%29%29%2F2%5C-3+=+0.154700538379251

Quadratic expression 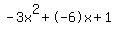-3x%5E2%2B-6x%2B1 can be factored:
-3x%5E2%2B-6x%2B1+=+-3%28x--2.15470053837925%29%2A%28x-0.154700538379251%29
Again, the answer is: -2.15470053837925, 0.154700538379251. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-3%2Ax%5E2%2B-6%2Ax%2B1+%29



Step 4. To find the y-intercept set x=0 in g(x)=y=-3x^2-6x+1

g%280%29=y=-3%2A0%5E2-6%2A0%2B1

or y=1.

The y-intercept is at (0,1) which is consistent with the above graph.


I hope the above steps and explanation were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

And good luck in your studies!

Respectfully,
Dr J
http://www.FreedomUniversity.TV