Question 224248: the length of a rectangle is increased by 120% and its width is decreased by 20%, what is the resulting percentage increase or decrease in the area? Justify your answer algebraically.
Found 2 solutions by drj, MathTherapy:
Answer by drj(1380)   (Show Source): (Show Source):
You can put this solution on YOUR website! The length of a rectangle is increased by 120% and its width is decreased by 20%, what is the resulting percentage increase or decrease in the area? Justify your answer algebraically.
Step 1. 120% means 1.2 and 20% means 0.20
Step 2. Let L be the original length and 1.20L be the increased length.
Step 3. Let w be the original width and (1-0.2)w=0.8w be the reduced width.
Step 4. Let w*L be the original area.
Step 5. Then, (0.8w)*(1.20L)=0.96w*L = (1-0.04)w*L
Step 6. ANSWER: The area is 96% of the original area or the area is reduced by 4%.
I hope the above steps were helpful.
For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Good luck in your studies!
Respectfully,
Dr J
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! the length of a rectangle is increased by 120% and its width is decreased by 20%, what is the resulting percentage increase or decrease in the area? Justify your answer algebraically.
Area of a rectangle = LW
If area is increased by 120%, then its new length is: 220% * L = 2.2L
Since its width is decreased by 20%, then its new width is: 80% * W = .8W
This makes its new area: 2.2L * .8W = 1.76LW
The difference in the original and new area is an increase of: 1.76 - 1, or .76
Therefore, the increase in its area is: 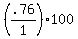 = =  % %
|
|
|