|
Question 223810: f (x) = x4 - 4x3-22x2 + 52x - 5
State approximately the intervals on which f is increasing and on which f is decreasing. Round your answers to the nearest tenth.
(leftmost increasing interval)(rightmost increasing interval)
(leftmost increasing interval)(rightmost increasing interval)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm not sure how to do this without using derivatives. So if you have not learned about derivatives the rest will not make much sense.
A function is increasing when its slope is positive. And we can find where a function's slope is positive by using the first derivative of the function.
So we'll start by finding the first derivative of f(x):
f'(x) = 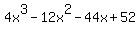
Next we will find the intervals where f'(x) is positive. In order to do this we need to factor f'(x). As usual, always start factoring by factoring out the Greatest Common Factor (GCF). The GCF for f'(x) is 4:
f'(x) = 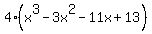
Next we try any of the other methods for factoring (patterns, trinomial factoring, factoring by grouping and trial and error of the possible rational roots. This expression,  , has too many terms for any of the patterns and for trinomial factoring. And factoring by grouping does not work. So we are left with trying the possible rational roots (which are +-1 and +-13). Trying 1 is easy (because all powers of 1 are 1) and, in this case, 1 does work! And when you find a root (let's call it "r"), it means (x-r) is a factor. So since 1 is a root, (x-1) is a factor. We can find the other factor using synthetic division: , has too many terms for any of the patterns and for trinomial factoring. And factoring by grouping does not work. So we are left with trying the possible rational roots (which are +-1 and +-13). Trying 1 is easy (because all powers of 1 are 1) and, in this case, 1 does work! And when you find a root (let's call it "r"), it means (x-r) is a factor. So since 1 is a root, (x-1) is a factor. We can find the other factor using synthetic division:
1 | 1 -3 -11 13
--- 1 -2 -13
---------------
1 -2 -13 0
So the other factor (which we find in front of the remainder above) is: 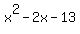 . Now we have: . Now we have:
f'(x) = 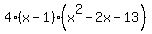
The quadratic factor at the end will not, unfortunately, factor easily. But since we really need all three roots, we can use the quadratic formula to find them. Using the quadratic formula on 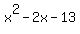 we get: we get:

So our fully factored first derivative is:
f'(x) = 
Next we will figure out when this is positive. To do so, it helps if we order the factors by the values of the roots (highest to lowest). The smallest root is 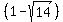 , the largest root is , the largest root is 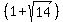 and the in between root is 1: and the in between root is 1:
f'(x) = 
The roots determine the boundaries of the intervals where f'(x) is positive and negative. So let's examine each interval and see whether f'(x) is positive or negative in each interval. And we do not need to find any specific values for f'(x). We only need to find the sign of f'(x) and we can do this by finding the sign of each factor. (The first factor listed below is 4 which is always positive. The other factors are listed in the order above.)
Interval factors of f'(x) f'(x)
x < 1-sqrt(14) + - - - -
1-sqrt(14) < x < 1 + + - - +
1 < x < 1+sqrt(14) + + + - -
x > 1+sqrt(14) + + + + +
So f'(x) is positive and f(x) is increasing on the intervals:
(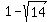 , 1) and ( , 1) and (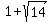 , ,  ) )
|
|
|
| |