Question 223755: A boat travels 9km upstream and 9km back. The time round trip takes 10hrs. The speed of the stream is 2km/hr. What is the speed of the boat in still water?
Answer by MLipsky(9)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For this problem, we need the distance formula: rt=d.
The current is 2 km/h. Even though we don't know the rate of the boat in still water, we know that going upstream, the rate can be expressed as: (r-2). Downstream, the rate is (r+2).
Now let's deal with "time":
(t-upstream) + (t-downstream) = 10
Rewrite: (t-downstream) = 10 - (t-upstream)
now, we can use that second equation to replace (t-downstream) in a minute.
Getting back to the original formula: rt=d, we get 2 equations:


There is our system of equations. Let's solve it with substitution. We can solve the first equation in terms of "t":
 (divided both sides by (r-2) ) (divided both sides by (r-2) )
Substitute that for "t" in the second equation. (This gets long-haired.)

 (FOIL) (FOIL)
 (added fractions) (added fractions)
 (subtracted 20 from both sides) (subtracted 20 from both sides)
Let's finally get rid of that complex fractions. Multiply every term by (r-2).

 (distributed (r-2) ) (distributed (r-2) )
 (combined like terms "r") (combined like terms "r")
 (added 11r, subtracted 22 from both sides) (added 11r, subtracted 22 from both sides)
That bad boy is a quadratic equation, and I can think of no better tool than the quadratic formula. Hopefully you are already familiar with the quadratic formula, because instead of showing it, I just plugged it into the handy dandy solver (results below). It gave me 2 values, but one of them was negative. How can the boat go a negative rate? That makes no sense in this problem. We can throw that out. That leaves the positive answer, 3.09, as the rate.
If you plug that in, you'll see it works. Also, it took the boat 8.23 hours upstream, and 1.77 hours downstream. (Holy cow! It would have been MUCH faster to walk!)
For tutoring, please visit 
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=1924 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 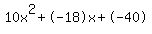 can be factored: can be factored:

Again, the answer is: 3.09317121994613, -1.29317121994613.
Here's your graph:
 |
|
|
|