Question 223687: A movie theater charges $7.50 for adutls and $4.50 for children. The receipts for one showing of a movie were $540. If 80 tickets were sold, find how many tickets of each type were sold.
Found 2 solutions by rfer, MLipsky:
Answer by rfer(16322)   (Show Source):
You can put this solution on YOUR website! you made a mistake in your setup.
7.5x+4.5y=540
x+y=80, y=80-x
---------------
7.5x+4.5(80-x)=540
7.5x+360-4.5x=540
3x=180
x=60
-------------------
7.50*60=$450
4.50*20=$90
total=$540
-------
I hope this helps.
Bob
Answer by MLipsky(9) (Show Source):
You can put this solution on YOUR website! I came up with a 6-step method for solving word problems:
1. Draw a picture.
2. Assign variables to all unknowns.
3. Write any relevant formulas.
4. Write an equation.
5. Solve the equation.
6. Check your solution.
1. Draw a picture.
(This is very useful for problems with shapes, distance, or combining mixtures.)
In this problem, drawing a picture probably wouldn't help.
2. Assign variables to all unknowns.
(The unknowns are usually what the question asks for, in the last part of the problem.)
The last part of the problem says, "find how many tickets of each type were sold." So we need variables for each type of ticket.
Let a = number of adult tickets.
Let c = number of child tickets.
3. Write any relevant formulas.
(Do you need  to solve this problem? How about  ? Write them down.)
In this problem, there aren't any relevant formulas.
4. Write an equation.
The problem says, "80 tickets were sold". So . . .
WARNING: a very common mistake in this problem would be to write . . .
. . . But "a" and "c" are the number of tickets sold, and the problem does not say that 540 tickets were sold. So what do we do with the rest of the numbers?
Each adult ticket cost $7.50. Let's think about that:
If they sold 1 adult ticket, they made 
If they sold 2 adult tickets, they made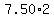 
If they sold "a" adult tickets, they made 
Make sense?
5. Solve the equation.
We have 2 equations:
You'll see this all the time in word problems: 2 equations, and 2 unknowns. You'll definitely want to know how to solve these. How?
Let's use substitution.
First, find the equation which looks simpler. Do you see it? The top equation looks simpler: Neither one of the variables has coefficients (numbers) in front of them.
Second, solve for one of the variables (get it alone). It doesn't matter which one you choose. I'll pick "a".
 (subtracted "c" from both sides)
(This says that "a" is the same as "80-c")
So, in our second equation,
, we can substitute "80-c" for "a". We get:
 That's substitution! Very cool. Make sense?
 (distributed 7.50)
 (combined like terms, "c")
 (subtracted 600 from both sides)
 (divided both sides by -3)
So, the number of child tickets is 20. If they sold 80 tickets total, there must have been 60 adult tickets. Want proof?
 (subtracted 20 from both sides)
6. Check your solution.
 Shazam! It checks.
For more worked problems, or tutoring, please visit MathLocker.com.
|
|
|
