|
Question 223601: factor by grouping:
6x^2+42x-5x-35
Found 3 solutions by checkley77, jsmallt9, MathTherapy:
Answer by checkley77(12844)   (Show Source):
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! Factoring by grouping is used on expressions of 4 or more terms. Here is a procedure for factoring by grouping:- Rewrite the expression as additions. Factoring by grouping requires the Commutative (reorder) and/or Associative (regroup) Properties so we cannot have subtractions.
- Group the terms into groups which can be factored. This may require reordering the terms
- Factor each group separately using any and all appropriate factoring techniques:
- Greatest Common Factor (GCF) (Note: Factoring by grouping is one of the few times where factoring out a 1 is done!)
- Factoring by patterns:
- Trinomial factoring
 - Factoring by grouping!
- Factoring by trial and error of the possible rational roots
- At this point your original expression has been regrouped and each of these groups has been factored. One of the following is true:
- There is a factor which common to each group. This is what you hope to happen. Proceed to the next step.
- A factor or its negative is common to each group. Examples:
- Factor: (x-3) Negative: (-x+3) or (3-x)
- Factor (2x+5) Negative: (-2x-5)
- Factor: (-4x-9) Negative: (4x+9)
In this case factor a -1 out of each group which has the negative factor. If done correctly you will now have a common factor in each group and you can proceed to the next step. - There is no factor nor its negative in each group. In this case you have start again at step #2 and try a different grouping. (Remember: Not all expressions will factor by grouping. Once you have tried all possible regroupings and you have not been able to get a common factor at this point, it is time to give up on factoring by grouping for this expression.
- Factor out the factor that is common to all groups. Until you get comfortable with this step, you might want to use a temporary variable. For example, let's say our factored groups look like:
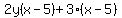 :- Our factor which is common to each group is (x-5).
- Let's use a temporary variable for this common factor: Let q = (x-5).
- Replace the common factor with the temporary variable:
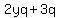 - Factor out the temporary variable: q(2y+3)
- Replace the temporary variable with the common factor: (x-5)(2y+3)
Eventually you will not need to use a temporary variable.
Now let's try this out on your expression:  :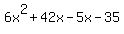
1. Rewrite as additions
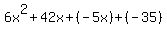
2. Create factorable groups. Since the first two terms have a common factor, 6x, and the last two terms also have a common factor, 5, we do not need to rearrange the terms. We'll just put parentheses around these two groups:
3. Factor out each group. We've already found GCF's for each group:
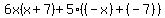
These groups will not factor any further so we will proceed to the next step.
4. Do we have a factor in each group which is common? The factors of the first group are 6x and (x+7). The factors of the second group are 5 and ((-x) + (-7)) so we not not have a factor common to both groups. Do we have a factor and its negative common to each group? Yes!! (x+7) and ((-x) + (-7)) are negatives of each other! So we'll factor out a -1 from the second group giving us:
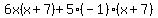
which simplifies to:
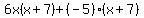
Now we have a common factor, (x+7), and we can proceed.
5. Factor out the common factor. (Use a temporary variable, if needed.)
Take a good look at this:- Can you see how this expression came from factoring out (x+7) from 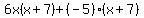? If not, then you should use a temporary variable for (x+7) as shown in the example in the procedure.
- Do you see that the original expression is now factored? IOW, we're done!
Since this and several other "factor by grouping" questions were posted within minutes of each other I am guessing that you posted all of them. Please try this procedure on the other problems. Repost the others if you can't figure them out.
Answer by MathTherapy(10557)  (Show Source):
|
|
|
| |
