Question 223539: What is the greatest prime you must consider to test whether 503 is prime? Why?
Please help! :)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! To make sense of the answer, let's look at the factors of 24:
1 24
2 12
3 8
4 6
6 4
8 3
12 2
24 1
As you look down this list of pairs of factors you will notice that the last half of the list is the same as the first half only in reverse order. There will be a "halfway" point for any list of factors for any number. If you are checking for divisibility there is no need to check beyond this "halfway" point because any factor found in the upper "half" is paired with a number in the lower "half" (which you would have already found).
So how do you determine the "halfway" point beyond which there is no point searching for more factors? Answer: The square root of the number you are trying to factor. Factors above the square root, if any, will always be paired with a factor below the square root. So there will be no factors above the square root that you would not have already found when checking the factors below the square root.
So for determining the primeness of 503, there is no point in checking prime factors above 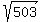 (which is approximately 22.4). The last prime before 22.4 is 19. So the only factors to check for 503 are: 2, 3, 5, 7, 11, 13, 17, 19. If none of these divide into 503, then 503 is prime. (which is approximately 22.4). The last prime before 22.4 is 19. So the only factors to check for 503 are: 2, 3, 5, 7, 11, 13, 17, 19. If none of these divide into 503, then 503 is prime.
|
|
|