|
Question 223022: what is the graph of the equation 6x^2-24x-5y^2-10y-11=0?
How do yo identify the solutions of the system of equations y^2-x^2=16
x^2-y^2=16
*Can you please show steps so i will know how to solve these kinds of problems in the future
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
From Wikipedia (see conic section article), if you have a conic of the form  , then one of the following is possible: , then one of the following is possible:
1) If 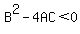 , then the equation represents an ellipse , then the equation represents an ellipse
Special Case: if  and and  , the equation represents a circle (which is a special case of an ellipse). , the equation represents a circle (which is a special case of an ellipse).
or...
2) If  , then the equation represents a parabola. , then the equation represents a parabola.
or...
3) if 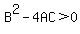 , then the equation represents a hyperbola. , then the equation represents a hyperbola.
Special Case: if  (ie (ie  ), then the conic is a rectangular hyperbola. ), then the conic is a rectangular hyperbola.
------------------------------------------------------------
Now let's solve the problem at hand.
 Start with the given conic. Start with the given conic.
 Rearrange the conic into the form Rearrange the conic into the form  . .
By looking at the last equation, we see that  , ,  , ,  , ,  , ,  and and  (just match up the corresponding coefficients). (just match up the corresponding coefficients).
So in order to classify the given conic, we're going to use the formula  and compare it to one of the cases described above. and compare it to one of the cases described above.
 Start with the given formula. Start with the given formula.
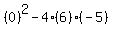 Plug in Plug in  , ,  , and , and  . .
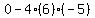 Square Square  to get to get  . .
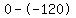 Multiply to get Multiply to get 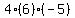 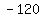 . .
 Combine like terms. Combine like terms.
So  . .
Since 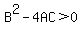 , this means that the conic is an hyperbola. , this means that the conic is an hyperbola.
Here's a graph to verify that result:

Graph of 
======================================================================
# 2
 Start with the first equation Start with the first equation
 Add Add  to both sides. to both sides.
--------
 Move onto the second equation. Move onto the second equation.
 Plug in Plug in 
 Distribute Distribute
 Combine like terms. Combine like terms.
Since the equation is NEVER true for any value of 'x' or 'y', this means that there are no solutions to the system. Visually, this means that the two graphs will NEVER intersect (ie cross).
|
|
|
| |