|
Question 222441: find three consecutive whole numbers such that twice the sum of the two smallest numbers is 10 more than three times the largest number
Answer by drj(1380)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find three consecutive whole numbers such that twice the sum of the two smallest numbers is 10 more than three times the largest number.
Step 1. Let n be an integer.
Step 2. Let n+1 and n+2 be the next two consecutive integers.
Step 3. Let n+n+1=2n+1 be the sum of the two smallest integers.
Step 4. Let 2(2n+1) be twice the sum of the two smallest integers.
Step 5. Let 3(n+2) be three times the largest number
Step 6. Then using Steps 3 and 4, 2(2n+1)=3(n+2)+10 since twice the sum of the two smallest numbers is 10 more than three times the largest number.
Step 7. Solving yields the following steps:
| Solved by pluggable solver: EXPLAIN simplification of an expression |
Your Result:
YOUR ANSWER
- This is an equation! Solutions: n=14.
- Graphical form: Equation
 was fully solved. was fully solved. - Text form: 2*(2n+1)=3*(n+2)+10 simplifies to 0=0
- Cartoon (animation) form:

For tutors: simplify_cartoon( 2*(2n+1)=3*(n+2)+10 )
- If you have a website, here's a link to this solution.
|
DETAILED EXPLANATION
Look at  . .
Moved these terms to the left  , ,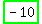
It becomes  . .
Look at  . .
Expanded term  by using associative property on by using associative property on 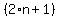
It becomes  . .
Look at  . .
Multiplied numerator integers
It becomes  . .
Look at  . .
Multiplied numerator integers
It becomes  . .
Look at  . .
Added fractions or integers together
It becomes  . .
Look at  . .
Moved  to the right of expression to the right of expression
It becomes  . .
Look at  . .
Removed extra sign in front of 
It becomes  . .
Look at  . .
Expanded term  by using associative property on by using associative property on 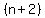
It becomes  . .
Look at  . .
Multiplied numerator integers
It becomes  . .
Look at  . .
Added fractions or integers together
It becomes  . .
Look at  . .
Removed extra sign in front of 
It becomes  . .
Look at  . .
Eliminated similar terms  , , replacing them with replacing them with 
It becomes  . .
Look at  . .
Remove extraneous '1' from product 
It becomes  . .
Look at  . .
Solved linear equation  equivalent to n-14 =0 equivalent to n-14 =0
It becomes  . .
Result: 
This is an equation! Solutions: n=14.
Universal Simplifier and Solver
Done!
|
n=14, then n+1=15 and n+2=16
Check original equation  or or  such that such that  which is a true statement. which is a true statement.
Step 8. ANSWER: The three consecutive integers are 14, 15, and 16.
I hope the above steps were helpful.
For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Good luck in your studies!
Respectfully,
Dr J
I hope the above steps were helpful.
For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Good luck in your studies!
Respectfully,
Dr J
|
|
|
| |