Question 221632: "write and solve an equation to find the nth term of each aritmetic sequence"
3,7,11,15, . . . n=8
10,5,0,-5, . . . n=21
34,49,64,79, . . . n=200
Found 2 solutions by stanbon, drj:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! "write and solve an equation to find the nth term of each arithmetic sequence"
---
Every arithmetic sequence has this form: a(n)= a(1)+(n-1)d
--------------------------------
3,7,11,15, . . . n=8
a(8) = 3 + 7*4 = 31
--------------------------
10,5,0,-5, . . . n=21
a(21) = 10 +(20)*-5 = 10-100 = -90
-------------------------------------
34,49,64,79, . . . n=200
a(200) = 34 + (199)*15 = 3019
============================================
Cheers,
Stan H.
Answer by drj(1380)   (Show Source): (Show Source):
You can put this solution on YOUR website! "Write and solve an equation to find the nth term of each arithmetic sequence"
Find the pattern or constant a to get the next term. So that
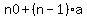
where a is a constant, n0 is the first term and n is the nth term.
We need (n-1) so when n=1 then n0 is the first term.
Step 1. 3,7,11,15, . . . n=8 3+(n-1)4=3+4n-4=4n-1.
ANSWER: 4n-1, at n=8 then 4*8-1=31
Step 2. 10,5,0,-5, . . . n=21 10-(n-1)5=10-5n-5=5-5n=5(1-n)
ANSWER: 5(1-n), at n=21 then 5(1-21)=100
Step 3. 34,49,64,79, . . . n=200 34+(n-1)15=34+15n-15=15n+19
ANSWER: 15n+19, at n=200 then 15*200+19=3000+19=3019.
I hope the above steps were helpful.
For free Step-By-Step Videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra or for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
And good luck in your studies!
Respectfully,
Dr J
drjctu@gmail.com
http://www.FreedomUniversity.TV
http://www.Facebook.com/FreedomUniversity.TV
http://www.Twitter.com/FreedomUTV
|
|
|