Question 221424: I am having a really hard time with proofs in geometry. This problem comes from the Essentials of Geometry for College Students; Chapter 2.5, exercise 19:
Given: Line Segment (LS) AB is congruent to LS DE; LS AB is perpendicular to LS BD; and, LS DE is perpendicular to LS BD.
Prove: LS AC is congruent to LS EC
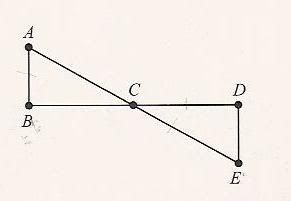
I can see that the figure is clearly 2 right angles adjacent to one another making them equal in measure; that point C is the midpoint of LS AE and LS DE as well as the vertex of both Triangles ABC and EDC. But, the trouble I'm having is putting them into a logical sequence. I know I have to prove one thing to move onto the next but putting them in the right order is difficult because there are so many ways to get the same answer. Can you help me with any tips that will make this process easier for me?
The answer to this specific question is given in the back of the book but I'm more interested in the process than the answer. I need to train my brain to think linearly which is what these types of exercises will do. The teacher I have isn't really helping much or should I say, isn't speaking in terms that are clicking with me.
I look forward to your response.
Thank you,
Cheri
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm having a hard time visualizing the problem. Can you post an image of it? If you need help posting images, check out this lesson.
The basic goal is to show that triangle ABC is congruent to triangle CED. From there, you can show that AC is congruent to EC because their corresponding parts are congruent.
Here's another way to prove this in a two column proof:

Notes:
1) CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent.
2) I used the theorems and postulates from this page and this page
3) In statement 5, recall that vertical angles are congruent to one another.
4) AAS stands for Angle Angle Side. I used the angles ACB and DCE for the first 'A', the angles ABC and CDE for the second 'A', the sides AB and DE for the 'S'
|
|
|