Question 220113: Find the measures of the three angles of a triangle if the second angle is 7 less than twice the first angle and the sum of the second and third angle is 22 less than three times the first angle. Recall that the angles of a triangle have a sum of 180 degrees.
Found 2 solutions by sloancm, MathTherapy:
Answer by sloancm(1)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Let the 1st angle be F
Since the 2nd angle is 7 less than twice the 1st, then 2nd angle = 2F - 7
Let the 3rd angle be T
Now, since the sum of the 2nd and 3rd angles is 22 less than three times the 1st, then we’ll have:
2F – 7 + T = 3F – 22. Solving for the 3rd angle, or T, we get: T = 3F – 2F – 22 + 7, or T = F - 15
Now, since we have the 3 angles, we set an equation equal to 180 (angles of a triangle are supplementary), as follows:
F + 2F – 7 + F – 15 = 180
F + 2F + F = 180 + 7 + 15
4F = 202
F =  =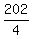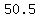 
Therefore, the 1st angle, or F = 
The 2nd angle, or 2F – 7 = 
The 3rd angle, or F – 15 = 
|
|
|
