|
Question 218172: I need help finding the equation of the upper half of the circle and the domain.

I am particularly having trouble finding the domain.
Thank you in advance.
Found 2 solutions by Theo, jsmallt9:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! equation of the circle is x^2 + y^2 = 10
solve for y:
y^2 = 10-x^2
y = +/- sqrt(10-x^2))
You want the upper half of the circle only, so you want:
y = sqrt(10-x^2))
You will reject y = -sqrt(10-x^2) because that would give you the bottom half of the circle which you don't want.
-----
Your domain is determined by sqrt(10-x^2))
Your domain has to result in real values of y in your range.
-----
If sqrt(10-x^2) is positive or 0, then your equation is valid because that would result in real values of y in your range.
----
If sqrt(10-x^2) is negative, then your equation is invalid because you would have the square root of a negative number which would not result in real values of y in your range.
-----
You need to find out when 10-x^2 is >= 0
-----
add x^2 to both sides of this equation to get:
10 >= x^2
-----
multiply both sides of this equation by -1 to get:
-10 <= -x^2
-----
add x^2 to both sides of this equation and add 10 to both sides of this equation to get:
x^2 <= 10
-----
Your domain will result in real values of y in your range when x^2 <= 10.
-----
x^2 is <= 10 when x < sqrt(10) and when -x > - sqrt(10)
Let x = sqrt(10), then x^2 = 10
Let x = -sqrt(10), then x^2 = 10
-----
Your domain is when -sqrt(10) <= x <= sqrt(10)
-----
A graph of your equation is shown below:
-----
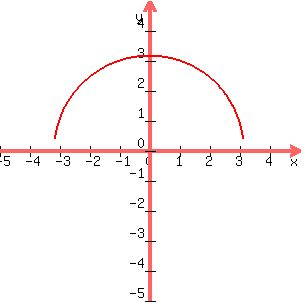
-----
since sqrt(10) = +/- 3.16227766, the graph looks accurate as far as the naked eye can see.
-----
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The upper half of a circle would be a function. So we sill start by writing the equation in the form of a function (i.e. we will solve for y):

Subtract  from both sides: from both sides:

Square root of each side:

(Sorry about the extra zero. Algebra.com's formula software can't handle +- without something in front of it.)
This is the equation of the entire circle. The upper half would be:
 (and the lower half (and the lower half 
As for the domain, we are looking for the set of all possible/allowable values for x. There are a couple of ways to find the domain of  : :- Graphically: Graph the circle (or half-circle) and determine what values x can be from the graph:
 From this we should be able to tell that x must be equal to or between -radius and +radius. And what is the radius of the circle? From the equation of the circle we should know that the radius is From this we should be able to tell that x must be equal to or between -radius and +radius. And what is the radius of the circle? From the equation of the circle we should know that the radius is  - Algebraically: With the square root, we must ensure that the radicand (the expression inside the square root) is either positive or zero. (IOW we cannot allow the radicand to become negative because there are no Real numbers whose squares are negative.)
So the domain is the set of all numbers which fit:

If you cannot "see" the domain from this then we have to solve this quadratic inequality. Solving quadratic inequalities is not easy. Perhaps the "easy" way is the factor  using the difference of squares pattern creatively: using the difference of squares pattern creatively:
 . This gives us: . This gives us:

This says that the product on the left is positive or zero. When are products positive or zero? Answer: When both factors are positive or both factors are negative or when one of the factors is zero. With these particular factors, it is impossible for them both to be negative because:- For
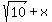 to be negative, x would have to be less than to be negative, x would have to be less than 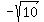 - If x is less than
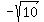 then the other factor, then the other factor, 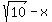 , would have to positive. (Think about subtracting a negative!) , would have to positive. (Think about subtracting a negative!)
So both factors must be positive or one of them must be zero:
 and and 
(The "or equal to" covers the possibility of zero factors.)
Solving these for x we get:
 and and 
Either way, the domain, in interval notation, is [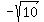 , ,  ] ]
|
|
|
| |