Question 217107: I am having difficulty with a question. The problems is as follows: A parabola has an x-intercept at 2, its axis of symmetry is the l ine x=4, and the y-coordinate of its vertex is 6. Determone the equation of the parabola.
I am setting up my equation - y = ax^2 + bx + c and plugging in the numbers as follows: y = 4a^2 + 2b + 8. Am I on the right track?
Thanks,
Lori
Found 3 solutions by RAY100, jsmallt9, Alan3354:
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! a rough sketch helps,,,,,
.
On x-y coordinates, line if symmetry is x=4, so draw a vertical at +4
.
We also know that the vertex is on the line of symmetry so (4,?) is vertex
.
But they give y=6 at vertex,,,,,therefore vertex is (4,6),,,might draw point
.
Since x intercept is 2,,,(1) we know(2,0) is point on curve,
.
(2) drawing point on rough graph, shows it to be curve pointing down.
.
.
The basic eqn is probably a y parabola pointing down ,,,,,,from sketch
.
base eqn is y=x^2 +b
.
expanded form is (y-k) = A(x-h)^2
.
we know vertex is (4,6) ,,,therefore h=4,,,k=6
.
subst,,,,(y-6)=A(x-4)^2,,,,,subst (2,0)
.
{(0)-6} =A {(2)-4}^2
.
-6 =A(-2)^2
.
-6 =A(4)
.
A=-6/4 = -3/2=-1.5,,,,,,note negative confirms pointing down parabola
.
combining,,,,(y-6)=-1.5(x-4)^2,,,,,answer
.
.
checking,,,,(2,0),,,,(0-6) =-1.5(2-4)^2,,,-6=-1.5(-2)^2 =-1.5*4=-6,,,ok
.
and (4,6),,,,,,6-6= -1.5(4-4)^2,,,,or 0=0,,,,,ok
.
.
in standard form,,,(y-6) = -1.5(x-4)^2
.
y-6 =-1,5{x^2-8x+16) = -1.5x^2 +12x -24
.
y= -1.5x^2 +12x -18,,,,,std form answer
.
checking,,,vertex x = -b/2a = -12/(2*-1.5) = +4 ,,,,,ok
.
y=-1.5(4)^2 +12(4) -18 = -24 +48-18=6,,,,ok
.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The key to this problem is to understand the symmetry of the parabola. The line of symmetry is x = 4. So the parabola to the left of x = 4 is a mirror image of the parabola to the right of x = 4.
So if there is an x-intercept at 2 (which is 2 to the left of 4), there will be another x-intercept at 6 (2 to the right of 4). So we have two x-intercepts: (2,0) and (6,0). We are also told that the vertex is (4, 6).
Now how do we get the equation? Here are a couple of ways:- Since the y-coordinates of the x-intercepts are zero we are looking for an
 that will be equal to zero when x = 2 and when x = 6. The simplest way to find this is to use: that will be equal to zero when x = 2 and when x = 6. The simplest way to find this is to use:
 . With some thought you should understand that if x=2 or x=6 then y = 0. Next we will use the other point, the vertex, to find the "a". Se will substitute 4 for the x and 6 for the y: . With some thought you should understand that if x=2 or x=6 then y = 0. Next we will use the other point, the vertex, to find the "a". Se will substitute 4 for the x and 6 for the y:
 and solve for a: and solve for a:



So our equation is: y = 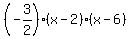 . If we want it in . If we want it in  form then we need to multiply out the right side giving: form then we need to multiply out the right side giving:
 - Another way to do this is to substitute the three points, one point at a time, into
 giving three equations: giving three equations:



Simplifying each we get:



We now have a system of three equations with three variables (a, b and c). There are a number of methods for solving systems like this, including Substitution, Linear Combination (aka Elimination or Addition), Kramer's rule (determinants) and a variety of matrix methods. Choose the one with which one you are most comfortable. It should result in the same a, b and c we found earlier.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am having difficulty with a question. The problems is as follows: A parabola has an x-intercept at 2, its axis of symmetry is the l ine x=4, and the y-coordinate of its vertex is 6. Determone the equation of the parabola.
I am setting up my equation - y = ax^2 + bx + c and plugging in the numbers as follows: y = 4a^2 + 2b + 8. Am I on the right track?
-------------------------
y = ax^2 + bx + c is the correct format.
------------------
Since the axis of symmetry is x=4, the other x-intercept will be at 6.
So the zeroes are 2 and 6.
The vertex at y = +6 and 2 x-intercepts means it opens downward.
The vertex is at (4,6), it has to be on the axis of symmetry.
--------------------
There's a way to find a parabola given 3 points (or a circle) using determinants. I'll send info on that to anyone interested.
--------------------
The x value at the vertex is -b/2a, so -b/2a = 4.
f(4) = 6 (vertex)
f(2) = 0
f(6) = 0
--------------
At x = 2:
4a + 2b + c = 0
At x = 6:
36a + 6b + c = 0
At x = 4
16a + 4b + c = 6
--------------
Solving 3 eqns in a, b and c gives:
a = -1.5
b = 12
c = -18
--> y = -1.5x^2 + 12x - 18
|
|
|