SOLUTION: Hi, I need some help with my American School Algebra 2 work. Given X^*3-4x^*2+2x+1=0 A. How many possible positive roots are there? B. How many possible negative roots are there

Algebra ->  Rational-functions -> SOLUTION: Hi, I need some help with my American School Algebra 2 work. Given X^*3-4x^*2+2x+1=0 A. How many possible positive roots are there? B. How many possible negative roots are there      Log On


   

Question 216529: Hi, I need some help with my American School Algebra 2 work. Given X^*3-4x^*2+2x+1=0
A. How many possible positive roots are there?
B. How many possible negative roots are there?
C. What are the possible rational roots?
D. Using synthetic substitution, which of the possible rational roots is actually a root of the equation?
E. Find the irrational roots of the equation(hint:ust the quadratic formula to solve the depressed equation.
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, I need some help with my American School Algebra 2 work.
Given x^3-4x^2+2x+1=0
A. How many possible positive roots are there?
Using Decartes' rule, there are either 2 or 0 positive roots.
-------------------
B. How many possible negative roots are there?
Descartes again, 1 negative root.
You can find Descartes on google.
-------------------
C. What are the possible rational roots?
+1 is a root. I found it by graphing the function.
Then dividing it out, you're left with
x^2-3x-1 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-3x%2B-1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-3%29%5E2-4%2A1%2A-1=13.

Discriminant d=13 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--3%2B-sqrt%28+13+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-3%29%2Bsqrt%28+13+%29%29%2F2%5C1+=+3.30277563773199
x%5B2%5D+=+%28-%28-3%29-sqrt%28+13+%29%29%2F2%5C1+=+-0.302775637731995

Quadratic expression 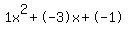1x%5E2%2B-3x%2B-1 can be factored:
1x%5E2%2B-3x%2B-1+=+%28x-3.30277563773199%29%2A%28x--0.302775637731995%29
Again, the answer is: 3.30277563773199, -0.302775637731995. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-3%2Ax%2B-1+%29

-----------
x = (3+sqrt(13))/2
x = (3-sqrt(13))/2
---------------------
D. Using synthetic substitution, which of the possible rational roots is actually a root of the equation?
E. Find the irrational roots of the equation(hint:ust the quadratic formula to solve the depressed equation.