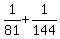SOLUTION: i'm confused as to how : the square root of (1/81)+(1/144) equates to the square root of 25/1296. is there something i'm missing?

Algebra ->  Square-cubic-other-roots -> SOLUTION: i'm confused as to how : the square root of (1/81)+(1/144) equates to the square root of 25/1296. is there something i'm missing?      Log On


   

Question 216467: i'm confused as to how : the square root of (1/81)+(1/144) equates to the square root of 25/1296. is there something i'm missing?
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Simply add the two fractions:

Solved by pluggable solver: Fractions Solver


1%2F81%2B1%2F144 Start with the given expression




In order to add these two fractions, these fractions need to have a common denominator.


In order to do that, we simply find that the LCM of 81 and 144 is 1296 (note: if you need help with finding the LCM, check out this solver)


Now we need to get each denominator to 1296



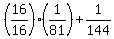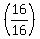
%2816%2F16%29%281%2F81%29%2B1%2F144 Multiply 1%2F81 by %2816%2F16%29


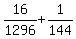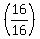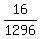
16%2F1296%2B1%2F144 Multiply 1%2F81 and %2816%2F16%29 to get 16%2F1296



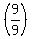
16%2F1296%2B%289%2F9%29%281%2F144%29 Multiply 1%2F144 by %289%2F9%29


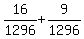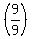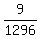
16%2F1296%2B9%2F1296 Multiply 1%2F144 and %289%2F9%29 to get 9%2F1296



Since both fractions have a common denominator of 1296, we can now combine the fractions


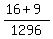%2816%2B9%29%2F1296 Combine the fractions


25%2F1296 Add the numerators



So

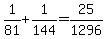
1%2F81%2B1%2F144=25%2F1296





Because 1%2F81%2B1%2F144=25%2F1296, this means sqrt%281%2F81%2B1%2F144%29=sqrt%2825%2F1296%29


You can take this even further by saying: sqrt%2825%2F1296%29=sqrt%2825%29%2Fsqrt%281296%29=5%2F36


So sqrt%281%2F81%2B1%2F144%29=5%2F36