Question 216460: Find all real and complex zeros for 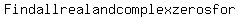 h(x)=x^3-x^2-7x-15 h(x)=x^3-x^2-7x-15
P: 1,3,5,15
Q:1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find all real and complex zeros for 
P: 1,3,5,15
Q:1
Since the function as you given it has no rational roots, I'm going to guess that you have a typo and  . If this is wrong, then stop reading (and you may need to repost your question). . If this is wrong, then stop reading (and you may need to repost your question).
With this h(x) we can find that -3 is a rational root. To illustrate I'll use synthetic division because it will also show how to factor h(x):
-3 | 1 -1 -7 15
---- -3 12 -15
-------------------
1 -4 5 0
The remainder, 0, tells us that h(-3) = 0. So -3 is a root of h(x). And if -3 is a root of h(x), then (x+3) is a factor of h(x). And the other factor is found in the numbers in front of the reaminder above, "1 -4 5", which translates into  . .
So  . The other roots for h(x) will come from the roots of . The other roots for h(x) will come from the roots of 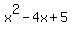 . This is a quadratic. Since it will not factor we'll use the quadratic formula: . This is a quadratic. Since it will not factor we'll use the quadratic formula:

For our expression, a = 1, b = -4 and c = 5. Substituting these into the formula we get:

Simplifying...



With the negative in the square root, we will have complex roots.




The 2's cancel leaving:

So our three roots are: -3, 2+i and 2-i
|
|
|