Question 216017: If there are 500 coins in total (consisting of half-dollars, dimes and pennies), and it totals $25.00, what is the combination of coins? How many half-dollars, dimes and pennies? Show the algebra.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! If there are 500 coins in total (consisting of half-dollars, dimes and pennies),
and it totals $25.00, what is the combination of coins?
How many half-dollars, dimes and pennies? Show the algebra.
:
Let h = no. of half dollars
Let d = no. of dimes
Let p = pennies
:
"If there are 500 coins in total"
h + d + p = 500
:
"it totals $25.00,"
.50h + .10d + .01p = 25
:
what is the combination of coins? How many half-dollars, dimes and pennies?
:
eliminate p and see what we can come up with, multiply the $$ equation by 100
Subtract the total coin equaion (makes .01p = p)
50h + 10d + p = 2500
h + d + p = 500
---------------------subtraction eliminates p
49h + 9d = 2000
9d = 2000 - 49h
d = 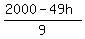
d has to be an integer and the number of half-dollars is low,
substitute values for h which will yield an integer value for d
Try h = 5
d = 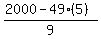
d = 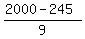
d = 
d = 195 dimes and 5 half dollars
:
Then: 500 - 195 - 5 = 300 pennies
:
5 half-dollars, 195 dimes, and 300 pennies
;
:
Check solution by finding the value
.5(5) + .10(195) + .01(300) =
2.50 + 19.50 + 3.00 = 25.00
:
:
An interesting note
I put this equation into the Ti83 and found there are 3 other solutions
for example:
14 half-dollars, 146 dimes and 340 pennies
23 half-dollars, 97 dimes and 380 pennies
32 half-dollars, 48 dimes and 420 pennies
|
|
|