SOLUTION: Factor the polynomial 15s^3-21s^2+18s

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Factor the polynomial 15s^3-21s^2+18s      Log On


   

Question 215406: Factor the polynomial
15s^3-21s^2+18s
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Factor the polynomial

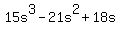
15s%5E3-21s%5E2%2B18s

Step 1. Factor out 3s in the three terms. That is, 3s%2A%285s%5E2-7s%2B6%29

Step 2. Need to find two integers m and n such that their product is mn=5*6=30 and their sum is m+n=-7.

Step 3. After several tries, the numbers are no numbers that satisfy step 2. Note if equation was 3s%2A%285s%5E2-7s-6%29 then the numbers would be -10 and 3 for the quadratic expression. We can factor with grouping where -7s=-10s%2B3s and

%285s%5E2-10s%29%2B%283s-6%29=+5s%28s-2%29%2B3%28s-2%29=%285s%2B3%29%28s-2%29.

Then the factor for this changed problem yields: 15s%5E3-21s%5E2-18s=3s%285s%2B3%29%28s-2%29


Step 4. We can use the quadratic formula given as

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=5, b=-7 and c=6.

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 5x%5E2%2B-7x%2B6+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-7%29%5E2-4%2A5%2A6=-71.

The discriminant -71 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -71 is + or - sqrt%28+71%29+=+8.42614977317636.

The solution is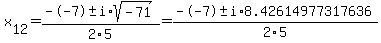

Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+5%2Ax%5E2%2B-7%2Ax%2B6+%29



Step 5. We have imaginary results for this example and there are no real solutons.

I hope the above steps and explanation were helpful.

For Step-By-Step videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonmetry please visit http://www.FreedomUniversity.TV/courses/Trignometry.

Also, good luck in your studies and contact me at john@e-liteworks.com for your future math needs.

Respectfully,
Dr J