Question 215208: Determine algebraically the point(s) if intersection of the graphs.
2x-y=-1
y=(x^2)+1|x+2|
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! If your problem is not


then stop reading and repost your question.
To solve this system, we will use the substitution method. The first step in the substitution method is to solve one of the equations for one of the variables. It does not matter which equation or which variable so it is to your advantage to find the easiest variable to solve for. Usually, a variable with a coefficient of 1 or -1 is the easiest to solve for.
Since the second equation is already solved for y we will use that.
The next step is to substitute for that variable in the other equation. So we will substitute for y in the first equation. When you make substitutions it is a good idea to surround your substitution with parentheses. So the first equation, after we subsitute for y, would become:

which simplifies to

Now we have an equation with just one variable to solve. Since we have an absolute value in the equation, we need to start by isolating it (so we can then get rid of it). To isolate the absolute value we'll add  and and  (one at a time or separately) which results in: (one at a time or separately) which results in:

To get rid of the minus sign in front of the absolute value we will multiply (or divide) both sides by -1 giving:

The absolute value is now isolated on the left side. We can now eliminate the absolute value. The general form for this step is:  can be rewritten as can be rewritten as  or or  . Using this on our equation we get: . Using this on our equation we get:
 or or 
These are both quadratic equations so we will solve them by getting one side equal to zero and then either factor the other side or use the quadratic formula. I prefer leading coefficients that are positive. They make factoring and the equadratic formula easier. So I will make one side of each equation zero while at the same time ensuring a positive leading coefficient. In the first equation I will add the opposite of every term on the right to both sides and in the second equation I will add the opposite of every term on the left side resulting in:
 or or 
Neither of these expressions will factor. So I'll use the quadratic formula on both:
 or or 
Simplifying we get:
 or or 
 or or 
 or or 
Because of the negative value in the square root of the first equation, we will not get any solutions from it.
We now have 2 possible x values (from the second equation). However, these x values do not fit the absolute value equation we had earlier:

For both of these x values, 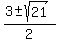 , the right side works out to be a negative number. (The work follows.) And the left side, an absolute value, cannot possibly be a negative number. So there are no solutions at all. These two graphs do not intersect. , the right side works out to be a negative number. (The work follows.) And the left side, an absolute value, cannot possibly be a negative number. So there are no solutions at all. These two graphs do not intersect.
Evaluating 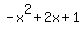 for for  : :
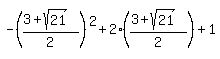
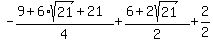
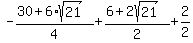
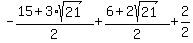
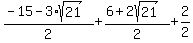
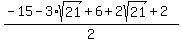
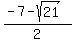 which is negative. which is negative.
Evaluating 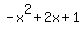 for for  : :
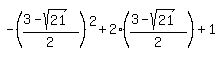
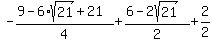
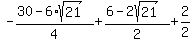
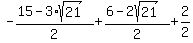
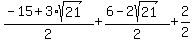
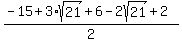
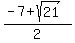 which is also negative. which is also negative.
|
|
|