SOLUTION: What are the four consecutive even integers that equal 308?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: What are the four consecutive even integers that equal 308?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 214726: What are the four consecutive even integers that equal 308?
Found 2 solutions by stanbon, drj:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
What are the four consecutive even integers that equal 308?
--------------------------
1st 2x-2
2nd 2x
3rd 2x+2
4th 2x+4
-----------------
Add to get:
8x +4 = 308
8x = 304
x = 38
-------------
2nd: 2x = 76
1st: 74
3rd: 78
4th: 80
=================
Cheers,
Stan H.

Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
What are the four consecutive even integers that equal 308?

Step 1. Let n be an even integer, n+2, n+4, and n+6 be the next three consecutive integers.

Step 2. Then n+n+2+n+4+n+6=308 as given by the problem statement where the sum of the four consecutive integers equal to 308.

Step 3. The following steps will solve the equation in Step 2:

Solved by pluggable solver: EXPLAIN simplification of an expression
Your Result:


YOUR ANSWER


  • This is an equation! Solutions: n=74.
  • Graphical form: Equation n%2Bn%2B2%2Bn%2B4%2Bn%2B6=308 was fully solved.
  • Text form: n+n+2+n+4+n+6=308 simplifies to 0=0
  • Cartoon (animation) form: simplify_cartoon%28+n%2Bn%2B2%2Bn%2B4%2Bn%2B6=308+%29
    For tutors: simplify_cartoon( n+n+2+n+4+n+6=308 )
  • If you have a website, here's a link to this solution.

DETAILED EXPLANATION

Look at n%2Bn%2Bhighlight_red%28+2+%29%2Bn%2Bhighlight_red%28+4+%29%2Bn%2Bhighlight_red%28+6+%29=308.
Added fractions or integers together
It becomes n%2Bn%2Bhighlight_green%28+12+%29%2Bn%2Bn=308.
Look at n%2Bn%2Bhighlight_red%28+12+%29%2Bn%2Bn=308.
Moved 12 to the right of expression
It becomes n%2Bn%2Bn%2Bn%2Bhighlight_green%28+12+%29=308.
Look at .
Eliminated similar terms highlight_red%28+n+%29,highlight_red%28+n+%29,highlight_red%28+n+%29,highlight_red%28+n+%29 replacing them with highlight_green%28+%281%2B1%2B1%2B1%29%2An+%29
It becomes highlight_green%28+%281%2B1%2B1%2B1%29%2An+%29%2B12=308.
Look at .
Added fractions or integers together
It becomes %28highlight_green%28+4+%29%29%2An%2B12=308.
Look at highlight_red%28+%28highlight_red%28+4+%29%29%2An+%29%2B12=308.
Remove unneeded parentheses around factor highlight_red%28+4+%29
It becomes highlight_green%28+4+%29%2An%2B12=308.
Look at 4%2An%2B12=highlight_red%28+308+%29.
Moved these terms to the left highlight_green%28+-308+%29
It becomes 4%2An%2B12-highlight_green%28+308+%29=0.
Look at 4%2An%2Bhighlight_red%28+12+%29-highlight_red%28+308+%29=0.
Added fractions or integers together
It becomes 4%2An%2Bhighlight_green%28+-296+%29=0.
Look at 4%2An%2Bhighlight_red%28+-296+%29=0.
Removed extra sign in front of 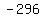-296
It becomes 4%2An-highlight_green%28+296+%29=0.
Look at highlight_red%28+4%2An-296+%29=0.
Solved linear equation highlight_red%28+4%2An-296=0+%29 equivalent to 4*n-296 =0
It becomes highlight_green%28+0+%29=0.
Result: 0=0
This is an equation! Solutions: n=74.

Universal Simplifier and Solver


Done!



Step 4. The integers are: 74, 76, 78, and 80.

I hope the above steps were helpful.

For free Step-By-Step Videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra or for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

And good luck in your studies!

Respectfully,
Dr J