Question 214343: Hi again, I asked this question some time ago, but had never got an answer, if anyone can help me I would be most grateful.
a) Find the area of the region bounded by the parabola:
f(x) 2x^2, g(x) = 3x^2 + 5 and the line y = 8.
b) Find dy/dx given that y = l+x(^2)e^(y)
Thanks again, Nick.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) Find the area of the region bounded by the parabola:
f(x) 2x^2, g(x) = 3x^2 + 5 and the line y = 8.
I think you have not typed the problem correctly. As stated, you have two parabolas and they do not intersect each other. So it not clear what the region is. See the graph below which include all three functions:

b) Find dy/dx given that y = l+x(^2)e^(y)
If we call  , ,  and and  , then u' = 0, v' = 2x and, using the chain rule, w' = y'* , then u' = 0, v' = 2x and, using the chain rule, w' = y'*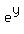 . Substituting u, v and w into the original equation we get: . Substituting u, v and w into the original equation we get:
y = u + v*w
Using basic rules of differentiation, we get:
y' = u' + v*w' + w*v'
Replacing u', v, v', w and w' (from above) we get:
y' = 0 +  *(y'* *(y'*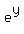 + + 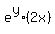
Now we use Algebra to simplify and solve for y':
y' = 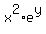 *y' + *y' + 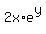
Subtract 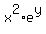 *y' from each side: *y' from each side:
y' - 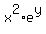 *y' = *y' = 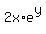
Factoring out y' on the left:
y'*
Dividing both sides by 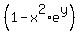 : :
y' = 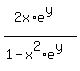
|
|
|