|
Question 214058: Suppose you get $1000 as a tax refund this year,and deposit in a retirement account earning 4.8% interest compounded monthly.then in the same retirement account you start to deposit $80.00 a month that you are saving because of some simple cuts that you have made in your budget,how much will you have in 25 years when you want to retire.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose you get $1000 as a tax refund this year,and deposit in a retirement account earning 4.8% interest compounded monthly.then in the same retirement account you start to deposit $80.00 a month that you are saving because of some simple cuts that you have made in your budget,how much will you have in 25 years when you want to retire.
-----
$1,000 invested in a retirement account for 25 years earning 4.1% compounded monthly will be worth $44,512.5051 at the end of 25 years from now.
-----
the formulas assume future value rather than future worth. they mean the same thing.
-----
You have two investments that can be handled separately and then combined together.
-----
The first is the money you invested today.
The formula for Future value of a Present Amount is:
-----

pa = $1,000
i = 4.1% / 12 / 100% = .00341666...
n = 25 * 12 = 300
-----
to compound the interest rate monthly you have to take the yearly interest rate and divide it by 12.
-----
to convert a percent to a rate you have to take the percent and divide it by 100%.
-----
that's the reason for taking 4.1% and dividing it by 12 and then dividing it by 100%.
-----
n is the number of time periods.
when you compound monthly, you are assuming 12 time periods per year.
you have to multiply the number of years by 12 to get the number of time periods required.
-----
interest rate divided by 12 results in time periods multiplied by 12 assuming you started off with interest rate per year and number of years.
-----
your future value of a present amount results in the formula of:
 being changed to: being changed to:
 = 2782.230482 = 2782.230482
-----
your $80.000 invested monthly is handled by the formula:
fv(pmt) = 
-----
this investment is also made monthly and compounded monthly.
the same interest rate and number of time periods applies.
investment at the end of each month is assumed.
we have:
pmt = $80.00
i = .00341666666667
n = 300
-----
placing these values into the formula gets:
fv(pmt) = 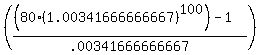 = 41730.27466 = 41730.27466
-----
rounded to the nearest cent, we have:
fv(pa) = $2,782.23
fv(pmt) = $41,730.27
-----
add these together to get a total future value of $44,512.50.
-----
there is no conflict with calculating these separately or combining them into one huge formula.
here's an example:
$1,000 invested at 12% compounded yearly for 3 years = $1,404.928
$500 invested each year for 3 years at 12% = $1,687.2
Total = $3,092.128
-----
let's look at how this would work out if we combined both these investments into one investment analyzed at the same time.
you invest $1,000
at the end of the first year you invest another $500.
total value at the end of the first year equals:
$1,000 * 1.12 + $500.00 = $1,620.00
-----
at the end of the second year you invest another $500.
total value at the end of the second year equals:
$1,620.00 * 1.12 + $500.00 = $2,314.40
-----
at the end of the third year you invest another $500.
total value at the end of the third year equals:
$2,314.40 + $500 = $3,092.128
-----
Whether you analyzed these separately as I did above, or you analyzed them together as I did just now, you got the same answer so the methods are equivalent.
-----
the reason we can do this is because:
(a + b) * c = a*c + b*c
which is the distributive law of arithmetic if you remember.
the combined analysis was (a+b)*c
the separate analysis was a*c + b*c
-----
|
|
|
| |