|
Question 213525: I need help with this problem. It has me so confused. x^4-7x^3+18x-126=0
Found 2 solutions by math problem solving, jsmallt9:
Answer by math problem solving(30)   (Show Source): (Show Source):
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! One way to solve polynomial equations like yours is to get one side equal to zero and then factor, if possible, the other side. Your equation already has one side equal to zero. So all we have to do is try to factor the left side.
There are many ways to factor:- Greatest Common Factor (GCF)
- Factor by patterns:
- Difference of Squares:
 - Sum of Cubes:
 - Difference of Cubes:
 - Perfect Square Trinomials:
- Trinomial Factoring
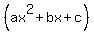 - Factoring by Grouping
- Factoring by trial and error of the possible rational roots
When factoring the only "rule" is to factor out the GCF (if it is not 1) first. After that, you use any and all other methods in any order and as many times as needed (including, possibly, the use of some methods more than once) until no more factoring can be done.
In your equation, the GCF of the left side is just 1 so we will not be factoring out a GCF. So now we need to figure out which, if any, of the other methods will work. You have 4 terms which is too many for any of the patterns and too many for Trinomial Factoring. So we are left with Factoring by Grouping and Trial and Error of Rational Roots. Neither is especially easy but I think Factoring by Grouping is the easier of the two so we will try it next:
To factor by grouping you have to group terms with a GCF together. (Remember the entire expression's GCF should be factored out already. But there may be GCF's for 1 or more subexpressions within the entire expression.) In order to do this grouping we need to be able to use the Associative Property. And we may need to rearrange the order with the Commutative Property in order to get terms with a GCF together. Both of these properties require that everything is an addition so we will start by rewriting your equation with additions:


Now we look for "groups" with GCF's. We should find that, without an rearranging of the order, the first two terms have a GCF and the last two terms also have a GCF. So we will group those pairs and factor out each group's GCF:


Now, if we're lucky, the non-GCF factors of each group match. And look, we're lucky! The non-GCF factors (in red) match:

We can now factor this common factor out of each group:

Neither of these two factors will factor further, no matter which method you try, so we're done factoring.
Now that we have factored the left side we are ready to find the solutions. The reason we get one side equal to zero and then factor the other side is that there is a special property we can use when we have a product (multiplication) which is equal to zero. It is called the Zero Product Property and it says that the only way for a product to be equal to zero is if one (or more) of the factors is zero. So if  , then, according to this property: , then, according to this property:
 or or 
Now we solve these separately. For the first equation we just add 7 to both sides giving us  . .
The second equation, since there are no squared or first power terms, is not especially difficult. First we subtract 18 from both sides:

And then we find the cube root of each side:


So we have found two solutions:
 or or 
In summary, to solve polynomial equations like this (with exponents greater than 1):- Get one side equal to zero.
- Factor the other side. (If you can't factor it you may not be able to solve it.)
- Use the Zero Product Property and set each individual factor equal to zero and solve those equations.
(Exception: If the highest exponent in the polynomial is 2, then you can use the Quadratic formula (or complete the square) at step 2 instead of factoring.)
|
|
|
| |