Question 212989: 3^2x+(3^x)-2=0?
My professor gave us a hint and said to change out the 3x for a u..? I think that confused me. I have tried to substitute the 3x for a u. Ex: 3^2x+u-2=0 but that does not make sense so i tried to use u(2-2)=0? I am so confused please help :)
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's another hint: we can rewrite 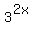 as as 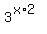 and and 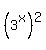 . In other words, . In other words, 
So  transforms into transforms into  . Now do you see how the substitution . Now do you see how the substitution  will help? will help? If not, then just repost or ask me.
---------------------------------------------------------------
New stuff....
 Start with the given equation. Start with the given equation.
 Rewrite Rewrite 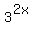 as as 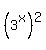 (see above). (see above).
Now let 
 Replace each Replace each 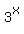 with 'u' with 'u'
Take note that we now have a much simpler quadratic to solve.
Notice that the quadratic 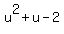 is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "u":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 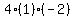 to get to get 
 Rewrite Rewrite 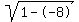 as as 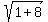
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the solutions (in terms of 'u') are  or or 
However, we want the solutions in terms of 'x'.
Let's find the solution of 'x' that corresponds to 
 Go back to the substitution equation. Go back to the substitution equation.
 Plug in Plug in 
 Rewrite Rewrite  as as  . Note: ANY number (except 0) to the 0th power is 1. . Note: ANY number (except 0) to the 0th power is 1.
Since the bases are equal, the exponents are equal. So  or or 
So the first solution is 
-----------------------------------------
Let's find the solution of 'x' that corresponds to 
 Go back to the substitution equation. Go back to the substitution equation.
 Plug in Plug in 
 Take the log of both sides. Take the log of both sides.
Since you CANNOT take the log of a negative number, this means that we cannot continue
So there isn't a corresponding solution of 'x' to 
============================================================
Answer:
So the only solution is 
Check:
 Start with the given equation. Start with the given equation.
 Plug in Plug in 
 Multiply Multiply
 Raise 3 to the zeroth power to get 1. Raise 3 to the zeroth power to get 1.
 Add Add
 Subtract. Subtract.
Since the equation is true, the solution  is verified. is verified.
|
|
|