Question 212804: the paddle wheel of a boat measures 16ft in diameter and is revolving at a rate of 20rpm.the maximum depth of the paddle wheel under water is 1 foot.suppose a point is located at the lowest point of the wheel at t=0.
use your function to find the height of the initial point after 5.5 seconds
a)7.5 ft
b)11 ft
c)10.4 ft
d)6.5 ft
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since the point on the wheel cycles regularly between a maximum (the top of the wheel) and a minimum (the bottom of the wheel) we will use sin or cos to model this problem. To model this we need to understand what the A, B, C and D represent in the general equation y = C + A*sin(B(x - D))
A = Amplitude
B = 2pi/period
C = Vertical shift (+ means shift up, - means shift down)
D = Horizontal shift (+ means shift right, - means shift left)
Since the wheel has a diameter of 16, the point on the wheel will range from 8 feet below the axle of the wheel to 8 feet above. This means the amplitude, A, should be 8.
Since there are 60 seconds in a minute then 20 rpm translates into one revolution every 3 seconds. The period, therefore, is 3 so our B should be 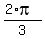
The vertical shift will be determined by whether we want y to represent the height of the point above the water or the height of the point above the axle. Assuming we want y to represent the height of the point above water and given that only one foot of the wheel is under water, then we want a vertical shift of 7 (since the radius is 8).
And finally the horizontal shift needs to be chosen based on the given point and based on whether we choose to use sin or cos. We are told that the point is at the lowest point on the wheel initially. In other words the initial point is (0, -1). So we have to figure out how to shift sin or cos so that we are at the minimum point at t = 0. Normally it takes 3/4 of a cycle for sin to reach its minimum and it takes cos 1/2 of a cycle to reach its minimum. So we would have to shift sin 3/4 to the left or cos 1/2 cycle to the left. In other words our D for sin would be -3/4(3) = -9/4 = -2.25 and for cos D would be -1/2(3) = -3/2 = -1.5. (We use negative for a left shift.)
Putting this all together we get:

or

And, if we're really clever, we would realize that since cos starts is cycle at a maximum, we could make it start at a minimum simply by making "A" negative. In other words we would not need a horizontal shift if "A" was negative:

In summary we have three equivalent equations we can use:



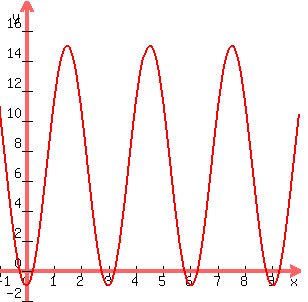
All three of these equations have the same graph (see below) and any one of them can be used to find the height of the point above water at any time. For t = 5.5:






or






or





So the answer is, after 5.5 seconds, the initial point is 3ft above the water (or 4ft below the axis of the wheel). (Why this answer does not match any of those provided I cannot say. I have checked my solution several times and I cannot find any errors. Either you have provided one or more incorrect numbers or the list of possible answers is incorrect.)
|
|
|